题目内容
14.已知直线y=x+1与x轴交于点A,抛物线y=-2x2的顶点平移后与点A重合.(1)求平移后的抛物线C的解析式;
(2)若点B(x1,y1),C(x2,y2)在抛物线C上,且-$\frac{1}{2}$<x1<x2,试比较y1,y2的大小.
分析 (1)求得A的坐标,然后根据平移的规律即可求得;
(2)根据二次函数的性质即可求解.
解答 解:(1)∵直线y=x+1与x轴交于点A,
∴A(-1,0),
∵抛物线y=-2x2的顶点平移后与点A重合,
∴平移后的抛物线C的解析式是y=-2(x+1)2;
(2)抛物线的对称轴为直线x=-1,抛物线开口向下,
故当-$\frac{1}{2}$<x1<x2,y1>y2.
点评 本题考查了二次函数图形与几何变化,二次函数图象上点的坐标特征,也考查了二次函数的性质.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
4. 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB.
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB.
(1)求证:PB是⊙O的切线;
(2)已知PA=2$\sqrt{3}$,BC=2.求⊙O的半径.
 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB.
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是⊙O外一点,PA切⊙O于点A,且PA=PB.(1)求证:PB是⊙O的切线;
(2)已知PA=2$\sqrt{3}$,BC=2.求⊙O的半径.
5.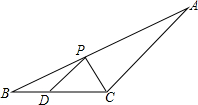 如图,△ABC中,∠ABC=30°,BC=6,点D是BC边上一点,且BD=2,点P是线段AB上一动点,则PC+PD的最小值为( )
如图,△ABC中,∠ABC=30°,BC=6,点D是BC边上一点,且BD=2,点P是线段AB上一动点,则PC+PD的最小值为( )
 如图,△ABC中,∠ABC=30°,BC=6,点D是BC边上一点,且BD=2,点P是线段AB上一动点,则PC+PD的最小值为( )
如图,△ABC中,∠ABC=30°,BC=6,点D是BC边上一点,且BD=2,点P是线段AB上一动点,则PC+PD的最小值为( )| A. | 2$\sqrt{7}$ | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
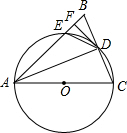 如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC、AC于点D、E,连接AD,过点D作DF⊥AB,垂足为点F.
如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC、AC于点D、E,连接AD,过点D作DF⊥AB,垂足为点F.