题目内容
11. 如图,直角三角形ABC的斜边AB=10,BC=5,∠ABC=60°.以点B为中心,将三角形ABC顺时针旋转120°,点A、C分别到达点E、D,则AC边扫过的面积(即图中阴影部分的面积)是多少?(结果保留π)
如图,直角三角形ABC的斜边AB=10,BC=5,∠ABC=60°.以点B为中心,将三角形ABC顺时针旋转120°,点A、C分别到达点E、D,则AC边扫过的面积(即图中阴影部分的面积)是多少?(结果保留π)
分析 根据扇形面积公式S=$\frac{nπ{R}^{2}}{360}$求出扇形ABE的面积和扇形CBD的面积,根据图形计算即可.
解答 解:∵AB=10,BC=5,∠C=90°,
∴AC=5$\sqrt{3}$,
△ABC的面积为$\frac{1}{2}$×AC×BC=$\frac{25\sqrt{3}}{2}$,
扇形ABE的面积为$\frac{120π×1{0}^{2}}{360}$=$\frac{100π}{3}$,
扇形CBD的面积为$\frac{120π×{5}^{2}}{360}$=$\frac{25π}{3}$,
∴AC边扫过的面积=$\frac{100π}{3}$+$\frac{25\sqrt{3}}{2}$-$\frac{25\sqrt{3}}{2}$-$\frac{25π}{3}$=25π.
点评 本题考查的是扇形面积的计算和旋转的性质,掌握扇形面积公式S=$\frac{nπ{R}^{2}}{360}$是解题的关键.

练习册系列答案
相关题目
 已知:如图,在△ABC中,AB=AC,AD,AE分别平分∠BAC和∠CAF,AD交BC于点D,AE=DC.求证:四边形ADCE是矩形.
已知:如图,在△ABC中,AB=AC,AD,AE分别平分∠BAC和∠CAF,AD交BC于点D,AE=DC.求证:四边形ADCE是矩形.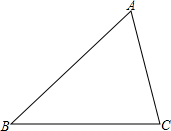 如图,△ABC,
如图,△ABC,