题目内容
16. 已知:如图,在△ABC中,AB=AC,AD,AE分别平分∠BAC和∠CAF,AD交BC于点D,AE=DC.求证:四边形ADCE是矩形.
已知:如图,在△ABC中,AB=AC,AD,AE分别平分∠BAC和∠CAF,AD交BC于点D,AE=DC.求证:四边形ADCE是矩形.
分析 由在△ABC中,AB=AC,AD是BC边的中线,可得AD⊥BC,即∠ADC=90°,再由AE平分∠CAF和∠CAF=2∠B,可证明AE∥DC,又因为AE=DC,所以四边形ADCE是平行四边形,再根据有一个角为直角的平行四边形即可证明四边形ADCE是矩形.
解答 证明:∵在△ABC中,AB=AC,AD是BC边的中线,
∴AD⊥BC,∠B=∠ACB,
∴∠ADC=90°,
∵AE为△ABC的外角∠CAF的平分线,
∴∠CAE=∠FAE, ∵∠FAC=∠B+∠ACB,
∵∠FAC=∠B+∠ACB,
∴∠FAC=2∠B,
∴∠FAE=∠B,
∴AE∥CD,
∵AE=DC,
∴四边形ADCE是平行四边形,
又∵∠ADC=90°,
∴四边形ADCE为矩形.
点评 此题考查了矩形的判定与性质、等腰三角形的性质:三线合一以及三角形中位线的性质.解答此类题的关键是要突破思维定势的障碍,运用发散思维,多方思考,探究问题在不同条件下的不同结论,挖掘它的内在联系,向“纵、横、深、广”拓展,从而寻找出添加的条件和所得的结论.

练习册系列答案
相关题目
7.对于一次函数y=x+6,下列结论错误的是( )
| A. | 函数值随自变量增大而增大 | |
| B. | 函数图象与两坐标轴围成的三角形面积为18 | |
| C. | 函数图象不经过第四象限 | |
| D. | 函数图象与x轴交点坐标是(0,-6) |
 如图,直角三角形ABC的斜边AB=10,BC=5,∠ABC=60°.以点B为中心,将三角形ABC顺时针旋转120°,点A、C分别到达点E、D,则AC边扫过的面积(即图中阴影部分的面积)是多少?(结果保留π)
如图,直角三角形ABC的斜边AB=10,BC=5,∠ABC=60°.以点B为中心,将三角形ABC顺时针旋转120°,点A、C分别到达点E、D,则AC边扫过的面积(即图中阴影部分的面积)是多少?(结果保留π)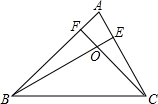 已知:如图,△ABC的两条高线BE,CF相交于点O.求证:∠BOC=180°-∠A(填空).
已知:如图,△ABC的两条高线BE,CF相交于点O.求证:∠BOC=180°-∠A(填空).