题目内容
n2-6n-k=1和n2-kn-7=0有一个共同的根,那么k的值为多少?(写下计算过程)
考点:一元二次方程的解
专题:
分析:两个方程联立后求得n的值,然后代入两个方程求得方程的解后验证答案即可.
解答:解:∵n2-6n-k=1和n2-kn-7=0有一个共同的根,
∴k≠6,
联立二方程得:
n2-6n-k-1=n2-kn-7,
即(k-6)n=k-6,
得n=1,
把1代入方程得1-6-k-1=0,即k=-6,
代入得二方程:
n2-6n+5=0,二根为1、5,
n2+6n-7=0,二根为1、-7,
可满足条件,
∴k值为-6.
∴k≠6,
联立二方程得:
n2-6n-k-1=n2-kn-7,
即(k-6)n=k-6,
得n=1,
把1代入方程得1-6-k-1=0,即k=-6,
代入得二方程:
n2-6n+5=0,二根为1、5,
n2+6n-7=0,二根为1、-7,
可满足条件,
∴k值为-6.
点评:本题考查了一元二次方程的解,解题的关键是根据两个方程共根确定n的值,难度中等.

练习册系列答案
相关题目

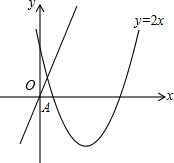 已知抛物线y=2x2+bx+6经过A(1,0),点P为抛物线的顶点,点B为抛物线与x轴的另一交点.
已知抛物线y=2x2+bx+6经过A(1,0),点P为抛物线的顶点,点B为抛物线与x轴的另一交点. 如图,长方形OABC在平面直角坐标系xOy的第一象限内,点A在x轴正半轴上,点C在y轴的正半轴上,点D、E分别是OC、BC的中点,∠CDE=30°,点E的坐标为(2,a).
如图,长方形OABC在平面直角坐标系xOy的第一象限内,点A在x轴正半轴上,点C在y轴的正半轴上,点D、E分别是OC、BC的中点,∠CDE=30°,点E的坐标为(2,a).