题目内容
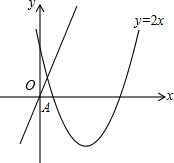 已知抛物线y=2x2+bx+6经过A(1,0),点P为抛物线的顶点,点B为抛物线与x轴的另一交点.
已知抛物线y=2x2+bx+6经过A(1,0),点P为抛物线的顶点,点B为抛物线与x轴的另一交点.(1)求出点P、点B的坐标.
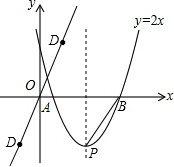
(2)如图,在直线y=2x上是否存在点D,使以O、P、B、D为顶点的四边形是平行四边形?若存在,求出点D的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:压轴题
分析:(1)把点A的坐标代入抛物线求出b的值,再整理成顶点式,然后写出点P的坐标;令y=0解方程即可得到点B的坐标;
(2)利用待定系数法求出直线BP的解析式,然后根据平行四边形对边平行且相等解答.
(2)利用待定系数法求出直线BP的解析式,然后根据平行四边形对边平行且相等解答.
解答:解:(1)∵抛物线y=2x2+bx+6经过A(1,0),
∴2×12+b+6=0,
解得b=-8,
∴y=2x2-8x+6=2(x-2)2-2,
∴顶点P的坐标为(2,-2),
令y=0,则2x2-8x+6=0,
解得x1=1,x2=3,
∴点B的坐标为(3,0);
(2)设直线BP的解析式为y=kx+b,
则
,
解得
,
所以,直线BP的解析式为y=2x-6,
∵直线y=2x与直线y=2x-6互相平行,
∴直线y=2x上是否存在点D,使以O、P、B、D为顶点的四边形是平行四边形,
此时,点D的坐标为(1,2)或(-1,-2).
∴2×12+b+6=0,
解得b=-8,
∴y=2x2-8x+6=2(x-2)2-2,
∴顶点P的坐标为(2,-2),
令y=0,则2x2-8x+6=0,
解得x1=1,x2=3,
∴点B的坐标为(3,0);

(2)设直线BP的解析式为y=kx+b,
则
|
解得
|
所以,直线BP的解析式为y=2x-6,
∵直线y=2x与直线y=2x-6互相平行,
∴直线y=2x上是否存在点D,使以O、P、B、D为顶点的四边形是平行四边形,
此时,点D的坐标为(1,2)或(-1,-2).
点评:本题是二次函数综合题型,主要利用了待定系数法求二次函数解析式,待定系数法求一次函数解析式,互相平行的直线的解析式的k值相等,平行四边形对边平行且相等,难点在于(2)根据坐标与图形性质利用点P、B的坐标特征分情况写出点D的坐标.

练习册系列答案
相关题目
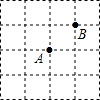 如图所示的是4×4的正方形网格,每个小正方形的顶点称为格点.若A、B为给定的格点,C为不同于A、B的任意一格点,以A、B、C三点构成三角形.
如图所示的是4×4的正方形网格,每个小正方形的顶点称为格点.若A、B为给定的格点,C为不同于A、B的任意一格点,以A、B、C三点构成三角形.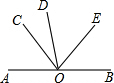 如图,A,O,B在一条直线上,AB⊥OD,且∠AOC=∠EOD.
如图,A,O,B在一条直线上,AB⊥OD,且∠AOC=∠EOD. 如图,已知线段AD=10cm,线段AC=BD=6cm,F是线段CD的中点,求线段BF的长.
如图,已知线段AD=10cm,线段AC=BD=6cm,F是线段CD的中点,求线段BF的长.