题目内容
(1)画出图1中△ABC的中线AD、角平分线AE和高线AF;
(2)在所画图形中,共有 个三角形,其中面积相等的三角形是 ;
(3)如图2,已知CD是△ABC的中线,DE是△ADC的中线,EF是△ADE的中线,若△AEF的面积是a,则△ABC的面积是 .

(2)在所画图形中,共有
(3)如图2,已知CD是△ABC的中线,DE是△ADC的中线,EF是△ADE的中线,若△AEF的面积是a,则△ABC的面积是

考点:作图—复杂作图,三角形的角平分线、中线和高,三角形的面积
专题:
分析:(1)利用三角形高线以及角平分线和中线的定义分别得出答案;
(2)利用三角形中线平分三角形面积进而得出答案;
(3)利用三角形中线平分三角形面积,以及相似三角形的性质得出即可.
(2)利用三角形中线平分三角形面积进而得出答案;
(3)利用三角形中线平分三角形面积,以及相似三角形的性质得出即可.
解答:解:(1)如图所示:
 ;
;
(2)在所画图形中,共有10个三角形,其中面积相等的三角形是:△ABD和△ADC;
故答案为:10;△ABD和△ADC;
(3)∵CD是△ABC的中线,DE是△ADC的中线,EF是△ADE的中线,△AEF的面积是a,
∴△DEF的面积是a,DE
BC,则S△ADE=2a,
∴
=
,
∴△ABC的面积是:8a.
故答案为:8a.
 ;
;(2)在所画图形中,共有10个三角形,其中面积相等的三角形是:△ABD和△ADC;
故答案为:10;△ABD和△ADC;
(3)∵CD是△ABC的中线,DE是△ADC的中线,EF是△ADE的中线,△AEF的面积是a,
∴△DEF的面积是a,DE
| ∥ |
. |
| 1 |
| 2 |
∴
| S△ADE |
| S△ABC |
| 1 |
| 4 |
∴△ABC的面积是:8a.
故答案为:8a.
点评:此题主要考查了复杂作图以及三角形中线的性质,正确运用三角形中线的性质是解题关键.

练习册系列答案
相关题目
永辉超市同时售出两台冷暖空调,每台均卖990元,按成本计算,其中一台盈利10%,另一台亏本10%,则出售这两台空调永辉超市( )
| A、不赔不赚 |
| B、赚20元 |
| C、赚90元 |
| D、亏20 元 |
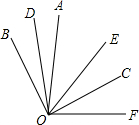 如图,OD,OC分别是∠AOB和∠EOF的角平分线,∠AOB=∠EOF.
如图,OD,OC分别是∠AOB和∠EOF的角平分线,∠AOB=∠EOF.