题目内容
 已知等腰梯形ABCD中,AD∥BC,∠B=45°,AD=2
已知等腰梯形ABCD中,AD∥BC,∠B=45°,AD=2| 3 |
A、2
| ||
B、2
| ||
C、2
| ||
D、2
|
考点:等腰梯形的性质
专题:
分析:由题意可知P点存在三次,AD中点正好有一次,求得∠APB=∠PBC=30°,根据特殊角的三角函数求得AM,根据等腰直角三角形性质求得AE=BE=DF=CF,设AE=BE=x,然后根据平行线分线段成比例定理得出
=
,从而求得AE=BE=DF=CF=1,BC=2
,即可求得梯形的面积;
| AP |
| BE |
| AM |
| ME |
| 3 |
解答: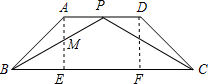 解:根据题意P点正好是AD的中点时∠BPC=120°,
解:根据题意P点正好是AD的中点时∠BPC=120°,
∴∠PBC=∠PCB=30°,AP=
AD=
-1,
∵等腰梯形ABCD中,AD∥BC,
∴∠APB=∠PBC=30°,
作AE⊥BC于E,DF⊥BC于F,
∵∠B=45°,
∴AE=BE=DF=CF,AM=
AP=
(
-1),
设AE=BE=x,
∵AD∥BC,
∴
=
,
即
=
,解得x=1,
∴AE=BE=DF=CF=1,BC=2
,
∴梯形ABCD的面积=
(AD+BC)•AE=
×(4
-2)×1=2
-1.
故选A.
 解:根据题意P点正好是AD的中点时∠BPC=120°,
解:根据题意P点正好是AD的中点时∠BPC=120°,∴∠PBC=∠PCB=30°,AP=
| 1 |
| 2 |
| 3 |
∵等腰梯形ABCD中,AD∥BC,
∴∠APB=∠PBC=30°,
作AE⊥BC于E,DF⊥BC于F,
∵∠B=45°,
∴AE=BE=DF=CF,AM=
| ||
| 3 |
| ||
| 3 |
| 3 |
设AE=BE=x,
∵AD∥BC,
∴
| AP |
| BE |
| AM |
| ME |
即
| ||
| x |
| ||||||
x-
|
∴AE=BE=DF=CF=1,BC=2
| 3 |
∴梯形ABCD的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故选A.
点评:本题考查了等腰梯形的性质,等腰直角三角形的性质,等腰三角形的性质,平行线的性质,平行线分线段成比例定理,特殊角的三角函数以及梯形的面积,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目

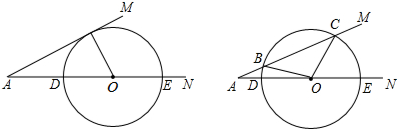
 如图,D为以AB为直径的半圆上的中点,C为AD弧上的点,弦BC、AD相交于点E,弦AC、BD的延长线相交于点F,求证:DE=DF.
如图,D为以AB为直径的半圆上的中点,C为AD弧上的点,弦BC、AD相交于点E,弦AC、BD的延长线相交于点F,求证:DE=DF.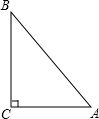 已知:如图,Rt△ABC中,∠C=90°,AC=6,AB=10.
已知:如图,Rt△ABC中,∠C=90°,AC=6,AB=10.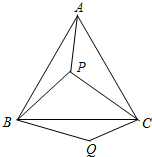 如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BP=BQ,连结CQ.
如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BP=BQ,连结CQ.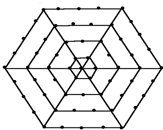 如图,有一个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推.
如图,有一个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推.