题目内容
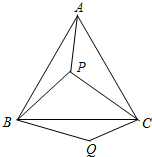 如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BP=BQ,连结CQ.
如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BP=BQ,连结CQ.(1)观察并猜想AP与CQ之间的大小关系,并说明理由.
(2)若PA=3,PB=4,PC=5,连结PQ,判断△PQC的形状并说明理由.
考点:全等三角形的判定与性质,等边三角形的判定与性质,勾股定理的逆定理
专题:
分析:(1)易证△ABP≌△CBQ,可得AP=CQ;
(2)根据PA=CQ,PB=BQ,即可判定△PQC为直角三角形.
(2)根据PA=CQ,PB=BQ,即可判定△PQC为直角三角形.
解答:解:(1)AP=CQ.理由如下:
∵∠PBQ=60°,且BQ=BP,
∴△BPQ为等边三角形,
∵∠ABP+∠CBP=60°,∠CBQ+∠CBP=60°,
∴∠CBQ=∠ABP,
在△ABP和△CBQ中,
,
∴△ABP≌△CBQ(SAS),
∴AP=CQ;
(2)∵等边△ABC和等边△BPQ中,
PB=PQ=4,PA=QC=3,
∵PQ2+CQ2=PC2,
∴△PQC为直角三角形(勾股定理逆定理).
∵∠PBQ=60°,且BQ=BP,
∴△BPQ为等边三角形,
∵∠ABP+∠CBP=60°,∠CBQ+∠CBP=60°,
∴∠CBQ=∠ABP,
在△ABP和△CBQ中,
|
∴△ABP≌△CBQ(SAS),
∴AP=CQ;
(2)∵等边△ABC和等边△BPQ中,
PB=PQ=4,PA=QC=3,
∵PQ2+CQ2=PC2,
∴△PQC为直角三角形(勾股定理逆定理).
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了勾股定理逆定理的运用,本题中求证△ABP≌△CBQ是解题的关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 已知等腰梯形ABCD中,AD∥BC,∠B=45°,AD=2
已知等腰梯形ABCD中,AD∥BC,∠B=45°,AD=2| 3 |
A、2
| ||
B、2
| ||
C、2
| ||
D、2
|
 如图,一张圆心角为45°的扇形纸板按如图方式剪得一个正方形,正方形的边长为1,则扇形纸板的面积是
如图,一张圆心角为45°的扇形纸板按如图方式剪得一个正方形,正方形的边长为1,则扇形纸板的面积是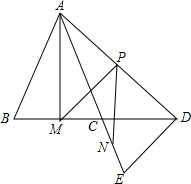 如图,已知AE与BD相交于点C,AB=AC,DE=DC,M、N、P分别是BC、CE、AD的中点.求证:
如图,已知AE与BD相交于点C,AB=AC,DE=DC,M、N、P分别是BC、CE、AD的中点.求证:
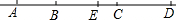 如图,B、C两点把线段AD分成2:3:4的三部分,点E是线段AD的中点,EC=2cm,求:
如图,B、C两点把线段AD分成2:3:4的三部分,点E是线段AD的中点,EC=2cm,求: