题目内容
能使式子
是一个实数的x的值有 个.
| -(x+1)2 |
考点:二次根式有意义的条件
专题:
分析:根据被开方数大于等于0解答.
解答:解:由题意得,-(x+1)2≥0,
所以,(x+1)2≤0,
∵(x+1)2≥0,
∴(x+1)2=0,
∴x=-1,
所以,x的值有1个.
故答案为:1.
所以,(x+1)2≤0,
∵(x+1)2≥0,
∴(x+1)2=0,
∴x=-1,
所以,x的值有1个.
故答案为:1.
点评:本题考查的知识点为:非负数的性质;二次根式的被开方数是非负数.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
在实数-
,
,π,
,0.1010010001…(每两个“1”之间依次多一个“0”)中,无理数有( )
| 1 |
| 3 |
| 2 |
| 9 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 已知等腰梯形ABCD中,AD∥BC,∠B=45°,AD=2
已知等腰梯形ABCD中,AD∥BC,∠B=45°,AD=2| 3 |
A、2
| ||
B、2
| ||
C、2
| ||
D、2
|
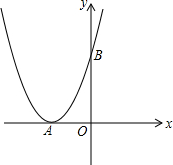 如图,已知二次函数y=(x+2)2的图象与x轴交于点A,与y轴交于点B.
如图,已知二次函数y=(x+2)2的图象与x轴交于点A,与y轴交于点B. 求如图中几何体的体积.
求如图中几何体的体积.