题目内容
如图，D为以AB为直径的半圆上的中点，C为AD弧上的点，弦BC、AD相交于点E，弦AC、BD的延长线相交于点F，求证：DE=DF．考点：圆周角定理,全等三角形的判定与性质,圆心角、弧、弦的关系
专题：证明题
分析：首先证明BD=AD，然后证明△BDE≌△ADF，即可解决问题．
解答：证明：∵点D为半圆上的中点，
∴
=
，
∴AD=BD；
又∵AB为半圆的直径，
∴∠ADF=∠ADB=90°；
在△BDE与△ADF中，
，
∴△BDE≌△ADF（ASA），
∴DE=DF．
证明：∵点D为半圆上的中点，∴
 |
| AD |
|
| BD |
∴AD=BD；
又∵AB为半圆的直径，
∴∠ADF=∠ADB=90°；
在△BDE与△ADF中，
|
∴△BDE≌△ADF（ASA），
∴DE=DF．
点评：该命题以圆为载体，重点考查了圆周角定理、全等三角形的判定及其性质等几何知识点；对分析问题解决问题的能力也提出了较高的要求．
练习册系列答案
相关题目
直角三角形纸片的两直角边长分别为6，8，现将△ABC如右图折叠，使点A和点B重合，则折痕DE的长是（ ）| A、3 | B、3.5 | C、3.75 | D、4 |
如图，一张圆心角为45°的扇形纸板按如图方式剪得一个正方形，正方形的边长为1，则扇形纸板的面积是
已知等腰梯形ABCD中，AD∥BC，∠B=45°，AD=2| 3 |
A、2
| ||
B、2
| ||
C、2
| ||
D、2
|
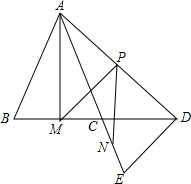如图，已知AE与BD相交于点C，AB=AC，DE=DC，M、N、P分别是BC、CE、AD的中点．求证：