题目内容
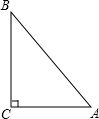 已知:如图,Rt△ABC中,∠C=90°,AC=6,AB=10.
已知:如图,Rt△ABC中,∠C=90°,AC=6,AB=10.(1)求BC的长;
(2)有一动点P从点C开始沿C→B→A方向以1cm/s的速度运动到点A后停止运动,设运动时间为t秒;求:
①当t为几秒时,AP平分∠CAB;
②当t为几秒时,△ACP是等腰三角形(直接写答案).
考点:勾股定理,角平分线的性质,等腰三角形的判定
专题:动点型
分析:(1)直接根据勾股定理求出BC的长即可;
(2)①过点P作PD⊥AB于点D,根据角平分线的性质可得出PD=PC,由HL定理可得出Rt△APD≌Rt△APC,故AD=AC,设PC=x,则PB=8-x,在Rt△BPD中根据勾股定理求出x的值即可得出结论;
②当点P在BC上时,只有AC=PC两种情况;当点P在AB上时,分AP=AC,PC=AC,AC=AP三种情况进行讨论.
(2)①过点P作PD⊥AB于点D,根据角平分线的性质可得出PD=PC,由HL定理可得出Rt△APD≌Rt△APC,故AD=AC,设PC=x,则PB=8-x,在Rt△BPD中根据勾股定理求出x的值即可得出结论;
②当点P在BC上时,只有AC=PC两种情况;当点P在AB上时,分AP=AC,PC=AC,AC=AP三种情况进行讨论.
解答:解:(1)∵Rt△ABC中,∠C=90°,AC=6,AB=10,
∴BC=
=
=8;
 (2)①如图1所示,
(2)①如图1所示,
过点P作PD⊥AB于点D,
∵AP平分∠CAB,
∴PD=PC.
在Rt△APD与Rt△APC中,
,
∴Rt△APD≌Rt△APC(HL),
∴AD=AC=6,
∴BD=10-6=4.
设PC=x,则PB=8-x,
在Rt△BPD中,PD2+BD2=PB2,即x2+42=(8-x)2,解得x=3,
∴当t=3秒时,AP平分∠CAB;
②如图2所示,
当点P在BC上时,
∵AC=P1C=6,
∴t=6秒;
当点P在AB上,AC=AP2时,
∵AC=AP2=6,
∴BC+BP2=8+4=12,
∴t=12秒;
当AC=P3C时,如图3所示,
过点D作CD⊥AB于点D,则AD=DP3,
∴
=
,即
=
,解得AD=3.6,
∴AP3=7.2,
∴BC+BP3=8+(10-7.2)=10.8,
∴t=10.8秒;
当CP4=AP4时,如图4所示,过点P4作P4E⊥AC于点E,
∵CP4=AP4,AC=6,
∴AE=
AC=3,
∴
=
,即
=
,解得AP4=5,
∴BC+BP4=8+(10-5)=13,
∴t=13秒.
综上所述,t=6或t=10.8或t=12或t=13秒时,△ACP是等腰三角形.
∴BC=
| AB2-AC2 |
| 102-62 |
 (2)①如图1所示,
(2)①如图1所示,过点P作PD⊥AB于点D,
∵AP平分∠CAB,
∴PD=PC.
在Rt△APD与Rt△APC中,
|
∴Rt△APD≌Rt△APC(HL),
∴AD=AC=6,
∴BD=10-6=4.
设PC=x,则PB=8-x,
在Rt△BPD中,PD2+BD2=PB2,即x2+42=(8-x)2,解得x=3,
∴当t=3秒时,AP平分∠CAB;
②如图2所示,

当点P在BC上时,
∵AC=P1C=6,
∴t=6秒;
当点P在AB上,AC=AP2时,
∵AC=AP2=6,
∴BC+BP2=8+4=12,
∴t=12秒;
当AC=P3C时,如图3所示,
过点D作CD⊥AB于点D,则AD=DP3,
∴
| AD |
| AC |
| AC |
| AB |
| AD |
| 6 |
| 6 |
| 10 |
∴AP3=7.2,
∴BC+BP3=8+(10-7.2)=10.8,
∴t=10.8秒;
当CP4=AP4时,如图4所示,过点P4作P4E⊥AC于点E,
∵CP4=AP4,AC=6,
∴AE=
| 1 |
| 2 |
∴
| AE |
| AP4 |
| AC |
| AB |
| 3 |
| AP4 |
| 6 |
| 10 |
∴BC+BP4=8+(10-5)=13,
∴t=13秒.
综上所述,t=6或t=10.8或t=12或t=13秒时,△ACP是等腰三角形.
点评:本题考查的是勾股定理,在解答此题时要注意进行分类讨论,不要漏解.

练习册系列答案
相关题目
 已知等腰梯形ABCD中,AD∥BC,∠B=45°,AD=2
已知等腰梯形ABCD中,AD∥BC,∠B=45°,AD=2| 3 |
A、2
| ||
B、2
| ||
C、2
| ||
D、2
|
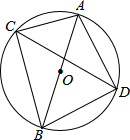 已知:如图所示,AB=10cm,BC=8cm,CD平分∠ACB.
已知:如图所示,AB=10cm,BC=8cm,CD平分∠ACB.

 如图,直角坐标系内的梯形AOBC,AC∥OB,AC、OB的长分别是关于x的方程x2-6mx+m2+4=0的两根,并且S△AOC:S△BOC=1:5.
如图,直角坐标系内的梯形AOBC,AC∥OB,AC、OB的长分别是关于x的方程x2-6mx+m2+4=0的两根,并且S△AOC:S△BOC=1:5.