题目内容
10. 如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.(1)求证:△DEF是等腰三角形;
(2)当∠A=45°时,求∠DEF的度数.
分析 (1)由AB=AC,∠ABC=∠ACB,BE=CF,BD=CE.利用边角边定理证明△DBE≌△CEF,然后即可求证△DEF是等腰三角形.
(2)根据∠A=45°可求出∠ABC=∠ACB=67.5°根据△DBE≌△CEF,利用三角形内角和定理即可求出∠DEF的度数.
解答 证明:∵AB=AC,
∴∠ABC=∠ACB,
在△DBE和△CEF中
$\left\{\begin{array}{l}{BE=CF}\\{∠ABC=∠ACB}\\{BD=CE}\end{array}\right.$,
∴△DBE≌△CEF,
∴DE=EF,
∴△DEF是等腰三角形;
(2)∵△DBE≌△CEF,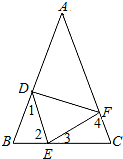
∴∠1=∠3,∠2=∠4,
∵∠A+∠B+∠C=180°,
∴∠B=$\frac{1}{2}$(180°-45°)=67.5°
∴∠1+∠2=112.5°
∴∠3+∠2=112.5°
∴∠DEF=67.5°
点评 此题主要考查学生对等腰三角形的判定与性质的理解和掌握,此题主要应用了三角形内角和定理和平角是180°,因此有一定的难度,属于中档题.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案
相关题目
15.下列说法中正确的是( )
| A. | 全等图形是指形状相同的两个图形 | B. | 全等三角形的面积和周长相等 | ||
| C. | 两个等边三角形是全等形 | D. | 全等图形是指面积相同的两个图形 |
2.下列方程中是一元二次方程的是( )
| A. | $3x-\frac{2}{x}=0$ | B. | ax2+bx+c=0 | C. | (3x-1)(2x+3)=0 | D. | (x+2)(x-7)=(x+1)(x-1) |
 如图,在四边形ABCD中,AB=BC,∠BAD+∠D=200°,∠C=80°,再添加一个条件,使△ABE≌△BCF,可添加的条件是BE=CF(写出一个即可)
如图,在四边形ABCD中,AB=BC,∠BAD+∠D=200°,∠C=80°,再添加一个条件,使△ABE≌△BCF,可添加的条件是BE=CF(写出一个即可)