题目内容
17.抛物线y=$\frac{1}{2}$x2-3的对称轴是y轴,y=-(x+$\frac{1}{3}$)2的对称轴是x=-$\frac{1}{3}$.分析 利用二次函数的顶点式可求得答案.
解答 解:
在y=$\frac{1}{2}$x2-3中,其顶点坐标为(0,-3),
∴其对称轴为x=0,即对称轴为y轴,
在y=-(x+$\frac{1}{3}$)2中,其顶点坐标为(-$\frac{1}{3}$,0),
∴其对称轴为x=-$\frac{1}{3}$,
故答案为:y轴;x=-$\frac{1}{3}$.
点评 本题主要考查二次函数的性质,掌握二次函数的顶点式是解题的关键,即在y=a(x-h)2+k中,其顶点坐标为(h,k),对称轴为x=h.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
8.下列“QQ表情”中属于轴对称图形的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
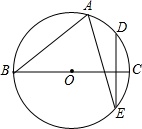 已知:如图,⊙O的直径BC=2,点A在⊙O上,∠ABC=30°,D是$\widehat{AC}$的中点,弦DE⊥BC,连接AE
已知:如图,⊙O的直径BC=2,点A在⊙O上,∠ABC=30°,D是$\widehat{AC}$的中点,弦DE⊥BC,连接AE ”表示为:abc;方框“
”表示为:abc;方框“ ”表示为:(xm+yn).例如:
”表示为:(xm+yn).例如: =1×19×3÷(24+31)=3.请根据这个规定解答下列问题:
=1×19×3÷(24+31)=3.请根据这个规定解答下列问题: =-$\frac{3}{2}$;
=-$\frac{3}{2}$; 为完全平方式,则k=±3;
为完全平方式,则k=±3; =6x2+7.
=6x2+7. 如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.
如图,在△ABC中,AB=AC,点D、E、F分别在AB、BC、AC边上,且BE=CF,BD=CE.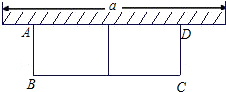 如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度为a为15米),围成中间隔有一道篱笆的长方形花圃.如果要围成面积为45平方米的花圃,AB的长是多少米?
如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度为a为15米),围成中间隔有一道篱笆的长方形花圃.如果要围成面积为45平方米的花圃,AB的长是多少米?