题目内容
9．等腰三角形的周长为16cm，底边长6cm，则底边上的高为4厘米．分析 根据等腰三角形的三线合一的性质和勾股定理进行求解．
解答 解：∵等腰三角形的周长为16cm，底边长6cm，
∴等腰三角形的腰长为（16-6）÷2=5，
∴底边上的高为$\sqrt{{5}^{2}-{3}^{2}}$=4厘米，
故答案为4．
点评 本题考查了勾股定理、等腰三角形三线合一定理．解题的关键是利用周长求出等腰三角形的腰长．
练习册系列答案
相关题目
19．
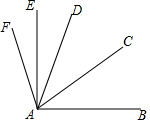如图，∠FAB=106°，AE是∠FAD的平分线，AC是∠DAB的平分线，∠EAD=20°．下列关系错误的是（ ）
如图，∠FAB=106°，AE是∠FAD的平分线，AC是∠DAB的平分线，∠EAD=20°．下列关系错误的是（ ）| A． | ∠FAD=40° | B． | ∠CAB=33° | C． | ∠FAB=2∠EDC | D． | ∠EAD与∠DAB互余 |
20．
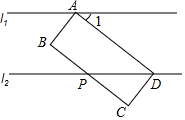如图，分别过矩形ABCD的顶点A、D作直线l1、l2，使l1∥l2，l2与边BC交于点P，若∠1=38°，则∠BPD为（ ）
如图，分别过矩形ABCD的顶点A、D作直线l1、l2，使l1∥l2，l2与边BC交于点P，若∠1=38°，则∠BPD为（ ）| A． | 162° | B． | 152° | C． | 142° | D． | 128° |
17．已知∠C=75°，则∠A与∠B满足以下哪个选项才能构成△ABC（ ）
| A． | sinA=$\frac{\sqrt{2}}{2}$，sinB=$\frac{\sqrt{2}}{2}$ | B． | cosA=$\frac{1}{2}$，cosB=$\frac{\sqrt{3}}{2}$ | C． | sinA=$\frac{\sqrt{2}}{2}$，tanB=$\sqrt{3}$ | D． | sinA=$\frac{\sqrt{3}}{2}$，cosB=$\frac{1}{2}$ |
如图，△ABC内接于圆O，半径R=$\sqrt{2}$+1，圆I过O，且与AB、AC相切，圆I的半径r=1，求证：圆I是△ABC的内切圆．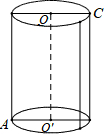
如图，有一个圆柱，它的高等于8cm，底面半径等于5cm，在圆柱的下底面点A处有一只蚂蚁，它想吃到上底面与点A相对的点C处的食物，需要爬行的最短路是多少？（π的值取3）