Question

11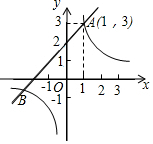．如图，已知一次函数y₁=x+m的图象与反比例函数y₂=$\frac{k}{x}$（k≠0）的图象交于A（1，3）．
（1）求这两个函数的关系式；
（2）若点B的坐标为（-3，-1），观察图象，写出y₁≥y₂的自变量的取值范围．

Answer 1

分析 （1）一次函数和反比例函数都是一个未知字母，把交点代入函数解析式即可；
（2）应从交点处看在交点的哪一边一次函数的函数值＞反比例函数的函数值．

解答 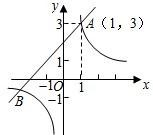解：（1）由题意，得3=1+m，
解得：m=2．
所以一次函数的解析式为y₁=x+2．
由题意，得3=$\frac{k}{1}$，
解得：k=3．
所以反比例函数的解析式为y₂=$\frac{3}{x}$．
由题意，得x+2=$\frac{3}{x}$，
解得x₁=1，x₂=-3．
当x₂=-3时，y₁=y₂=-1，
所以交点B（-3，-1）．

（2）由图象可知，当-3≤x＜0或x≥1时，函数值y₁≥y₂．

点评 本题考查用待定系数法求函数解析式；需注意：无论是自变量的取值范围还是函数值的取值范围，都应该从交点入手思考．