题目内容
4.解方程组:$\left\{\begin{array}{l}{x+y=1}\\{3x-2y=13}\end{array}\right.$.分析 根据代入消元法,可得答案.
解答 解:$\left\{\begin{array}{l}{x+y=1①}\\{3x-2y=13②}\end{array}\right.$
由①得
x=1-y③,
把③代入②,得
3(1-y)-2y=13,
解得y=-2,
把y=-2代入③,得
x=3,
原方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$.
点评 本题考查了解方程组,利用代入消元法得出方程组的解是解题关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
15.已知$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b为常数,且ab≠0)表示焦点在x轴上的双曲线,若$\frac{{x}^{2}}{m+3}$+$\frac{{y}^{2}}{2m-4}$=1表示焦点在x轴上的双曲线,则m的取值范围是( )
| A. | m>2 | B. | m>-3 | C. | m≥-3 | D. | -3<m<2 |
13. 如图,在平面直角坐标系中,已知A(-5,0),B(5,0),C(3,6),则△ABC重心的坐标是( )
如图,在平面直角坐标系中,已知A(-5,0),B(5,0),C(3,6),则△ABC重心的坐标是( )
 如图,在平面直角坐标系中,已知A(-5,0),B(5,0),C(3,6),则△ABC重心的坐标是( )
如图,在平面直角坐标系中,已知A(-5,0),B(5,0),C(3,6),则△ABC重心的坐标是( )| A. | ($\frac{1}{3}$,1) | B. | ($\frac{2}{3}$,1) | C. | (1,$\frac{2}{3}$) | D. | (1,2) |
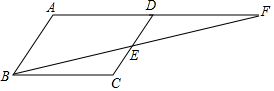 在?ABCD中,E为CD的中点,连接BE并延长交AD的延长线于F.求证:AD=DF.
在?ABCD中,E为CD的中点,连接BE并延长交AD的延长线于F.求证:AD=DF.