题目内容
10.求值或计算:①求满足条件的x值:$\frac{1}{4}$x2-16=0
②计算:$\sqrt{(-4)^{2}}$-$\root{3}{-27}$-$\sqrt{25}$.
分析 ①方程整理后,利用平方根定义开方即可求出解;
②原式利用平方根、立方根定义计算即可得到结果.
解答 解:①方程整理得:x2=64,
解得:x=8或x=-8;
②原式=4+3-5=2.
点评 此题考查了实数的运算,以及平方根,熟练掌握运算法则是解本题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
20.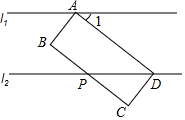 如图,分别过矩形ABCD的顶点A、D作直线l1、l2,使l1∥l2,l2与边BC交于点P,若∠1=38°,则∠BPD为( )
如图,分别过矩形ABCD的顶点A、D作直线l1、l2,使l1∥l2,l2与边BC交于点P,若∠1=38°,则∠BPD为( )
 如图,分别过矩形ABCD的顶点A、D作直线l1、l2,使l1∥l2,l2与边BC交于点P,若∠1=38°,则∠BPD为( )
如图,分别过矩形ABCD的顶点A、D作直线l1、l2,使l1∥l2,l2与边BC交于点P,若∠1=38°,则∠BPD为( )| A. | 162° | B. | 152° | C. | 142° | D. | 128° |
15.已知$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b为常数,且ab≠0)表示焦点在x轴上的双曲线,若$\frac{{x}^{2}}{m+3}$+$\frac{{y}^{2}}{2m-4}$=1表示焦点在x轴上的双曲线,则m的取值范围是( )
| A. | m>2 | B. | m>-3 | C. | m≥-3 | D. | -3<m<2 |
20. 如图,AD∥BC,若∠1=36°,则∠2的度数是( )
如图,AD∥BC,若∠1=36°,则∠2的度数是( )
 如图,AD∥BC,若∠1=36°,则∠2的度数是( )
如图,AD∥BC,若∠1=36°,则∠2的度数是( )| A. | 144° | B. | 126° | C. | 64° | D. | 36° |
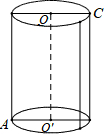 如图,有一个圆柱,它的高等于8cm,底面半径等于5cm,在圆柱的下底面点A处有一只蚂蚁,它想吃到上底面与点A相对的点C处的食物,需要爬行的最短路是多少?(π的值取3)
如图,有一个圆柱,它的高等于8cm,底面半径等于5cm,在圆柱的下底面点A处有一只蚂蚁,它想吃到上底面与点A相对的点C处的食物,需要爬行的最短路是多少?(π的值取3)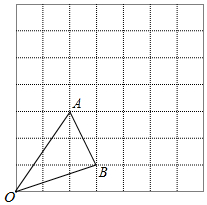 如图,在7×7的正方形网格中有一△OAB,其中点O、A、B均在图中格点上,观察图形并按要求回答问题:
如图,在7×7的正方形网格中有一△OAB,其中点O、A、B均在图中格点上,观察图形并按要求回答问题: