题目内容
12.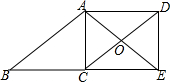 如图,四边形ABCD是平行四边形,点E在BC的延长线上,且CE=BC,AE=AB,AE、DC相交于点O,连接DE.
如图,四边形ABCD是平行四边形,点E在BC的延长线上,且CE=BC,AE=AB,AE、DC相交于点O,连接DE.(1)求证:四边形ACED是矩形;
(2)若∠AOD=120°,AC=4,求对角线CD的长.
分析 (1)根据平行四边形的性质得出AD∥BC,AD=BC,AB=DC,求出AD=CE,AD∥CE,AE=DC,根据矩形的判定得出即可;
(2)根据矩形的性质得出OA=$\frac{1}{2}$AE,OC=$\frac{1}{2}$CD,AE=CD,求出OA=OC,求出△AOC是等边三角形,即可得出答案.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,AB=DC,
∵CE=BC,
∴AD=CE,AD∥CE,
∴四边形ACED是平行四边形,
∵AB=DC,AE=AB,
∴AE=DC,
∴四边形ACED是矩形;
(2)解:∵四边形ACED是矩形,
∴OA=$\frac{1}{2}$AE,OC=$\frac{1}{2}$CD,AE=CD,
∴OA=OC,
∵∠AOC=180°-∠AOD=180°-120°=60°,
∴△AOC是等边三角形,
∴OC=AC=4,
∴CD=8.
点评 本题考查了矩形的性质和判定,平行四边形的性质,等边三角形的性质和判定的应用,能综合运用定理进行推理是解此题的关键.

练习册系列答案
相关题目
1.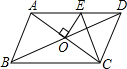 如图,?ABCD的周长为16cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
如图,?ABCD的周长为16cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
 如图,?ABCD的周长为16cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
如图,?ABCD的周长为16cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )| A. | 6cm | B. | 8cm | C. | 10cm | D. | 12cm |
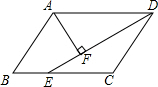 如图,?ABCD中,DE平分∠ADC交BC于E,AF⊥DE于F,已知∠DAF=58°,则∠B=64°.
如图,?ABCD中,DE平分∠ADC交BC于E,AF⊥DE于F,已知∠DAF=58°,则∠B=64°.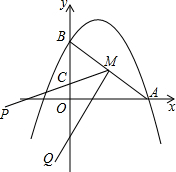 如图,抛物线y=-$\frac{1}{2}$x2+x+4与x轴和y轴的正半轴分别交于点A和B.
如图,抛物线y=-$\frac{1}{2}$x2+x+4与x轴和y轴的正半轴分别交于点A和B. 在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
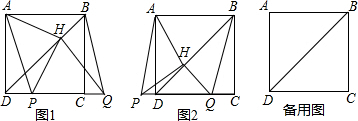
在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF. 如图,MN与BC在同一条直线上,且MN=BC=2,点B和点N重合,以MN为底作高为2的等腰△PMN,以BC为边作正方形ABCD,若设△PMN沿射线BC方向平移的距离为x,两图形重合部分的面积为y,则y关于x的函数大致图象是( )
如图,MN与BC在同一条直线上,且MN=BC=2,点B和点N重合,以MN为底作高为2的等腰△PMN,以BC为边作正方形ABCD,若设△PMN沿射线BC方向平移的距离为x,两图形重合部分的面积为y,则y关于x的函数大致图象是( )