题目内容
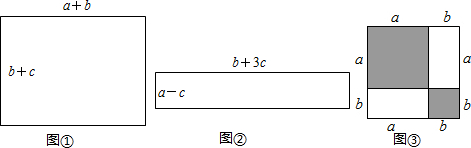
11.我们在分析解决某些数学问题时,经常要比较两个数或代数的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号来确定它们的大小,即要比较代数式M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N.若M-N=0,则M=N.若M-N<0,则M<N.请你用“作差法”解决以下问题:(1)如图,试比较图①、图②两个矩形的周长C1、C2的大小(b>c);
(2)如图③,把边长为a+b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个矩形,试比较两个小正方形的面积之和S1与两个矩形面积之和S2的大小.
分析 (1)根据题意用整式表示出C1和C2,求差即可;
(2)根据题意、结合图形表示出S1和S2,求差,根据偶次方的非负性解答.
解答 解:(1)C1-C2=2(a+b+b+c)-2(b+3c+a-c)=2a+4b+2c-2b-2a-4c=2(b-c),
∵b>c,
∴2(b-c)>0,即C1-C2,>0,
∴C1>C2;
(2)S1-S2=(a2+b2)-(ab+ab)=a2+b2-2ab=(a-b)2≥0,
则S1≥S2.
点评 本题考查的是整式的混合运算,掌握整式的混合运算法则、完全平方公式、灵活运用数形结合思想是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.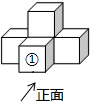 如图所示的几何体是由5个大小相同的小正方体摆成的,若取走小正方体①,下列说法正确的是( )
如图所示的几何体是由5个大小相同的小正方体摆成的,若取走小正方体①,下列说法正确的是( )
 如图所示的几何体是由5个大小相同的小正方体摆成的,若取走小正方体①,下列说法正确的是( )
如图所示的几何体是由5个大小相同的小正方体摆成的,若取走小正方体①,下列说法正确的是( )| A. | 主视图与左视图不变 | B. | 左视图与俯视图不变 | ||
| C. | 主视图与俯视图改变 | D. | 左视图与俯视图改变 |
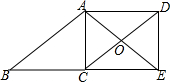 如图,四边形ABCD是平行四边形,点E在BC的延长线上,且CE=BC,AE=AB,AE、DC相交于点O,连接DE.
如图,四边形ABCD是平行四边形,点E在BC的延长线上,且CE=BC,AE=AB,AE、DC相交于点O,连接DE.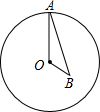 如图,点A为⊙O上一个动点,点B在⊙O内,且OA=2$\sqrt{3}$,OB=2,当∠OAB的度数取最大值时,AB的长度为2$\sqrt{2}$.
如图,点A为⊙O上一个动点,点B在⊙O内,且OA=2$\sqrt{3}$,OB=2,当∠OAB的度数取最大值时,AB的长度为2$\sqrt{2}$.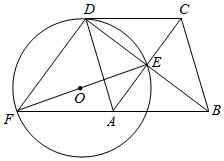 如图,菱形ABCD的对角线AC、BD相交于点E,F是BA延长线上一点,连接EF,以EF为直径作⊙O.
如图,菱形ABCD的对角线AC、BD相交于点E,F是BA延长线上一点,连接EF,以EF为直径作⊙O.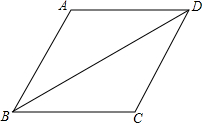 如图,菱形ABCD的周长为20,对角线BD=8,求sin∠ABD的值.
如图,菱形ABCD的周长为20,对角线BD=8,求sin∠ABD的值.