题目内容
19.定义:如果一元二次方程ax2+bx+c=o(a≠0)满足a-b+c=0,那么我们称这个方程为“蝴蝶”方程.已知关于x的方程ax2+bx+c=0(a≠0)是“蝴蝶”方程,且有两个相等的实数根,则下列结论中正确的是( )| A. | b=c | B. | a=b | C. | a=c | D. | a=b=c |
分析 根据已知得出方程ax2+bx+c=0(a≠0)有x=-1,再判断即可.
解答 把x=-1代入方程ax2+bx+c=0得出a-b+c=0,
∴b=a+c,
∵方程有两个相等的实数根,
∴△=b2-4ac=(a+c)2-4ac=(a-c)2=0,
∴a=c,
故选C.
点评 本题考查了一元二次方程的解,根的判别式,根与系数的关系的应用,主要考查学生的理解能力和计算能力.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
10.将$\frac{3a}{a-b}$中的a、b都变为原来的3倍,则分式的值( )
| A. | 不变 | B. | 扩大为原来的3倍 | C. | 扩大为原来的9倍 | D. | 缩小到原来的$\frac{1}{3}$ |
14. 如图,线段CD两个端点的坐标分别为C(1,2),D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B的坐标为(6,0),则点A的坐标为
如图,线段CD两个端点的坐标分别为C(1,2),D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B的坐标为(6,0),则点A的坐标为
( )
 如图,线段CD两个端点的坐标分别为C(1,2),D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B的坐标为(6,0),则点A的坐标为
如图,线段CD两个端点的坐标分别为C(1,2),D(2,0),以原点为位似中心,将线段CD放大得到线段AB,若点B的坐标为(6,0),则点A的坐标为( )
| A. | (2,5) | B. | (2.5,5) | C. | (3,5) | D. | (3,6) |
4.小明和3个女生、4个男生玩丢手绢的游戏,如果小明随意将手绢丢在一名同学后面,那么这名同学不是女生的概率是( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{4}{7}$ | D. | $\frac{3}{7}$ |
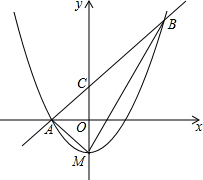 如图,顶点M在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,点B的横坐标为2,连接AM、BM.
如图,顶点M在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,点B的横坐标为2,连接AM、BM.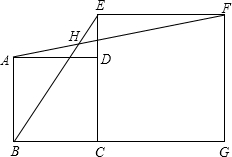 已知,如图,四边形ABCD和四边形ECGF都是正方形,连接BE、AF,求证:∠EHF=45°.
已知,如图,四边形ABCD和四边形ECGF都是正方形,连接BE、AF,求证:∠EHF=45°.