题目内容
7.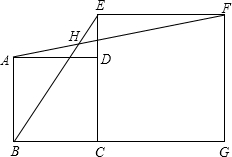 已知,如图,四边形ABCD和四边形ECGF都是正方形,连接BE、AF,求证:∠EHF=45°.
已知,如图,四边形ABCD和四边形ECGF都是正方形,连接BE、AF,求证:∠EHF=45°.
分析 连接AC、CF,如图,先利用正方形的性质得∠DAC=∠ACB=∠ACE=∠ECF=45°,AC=$\sqrt{2}$BC,CF=$\sqrt{2}$CE,则∠ACF=90°,于是可根据相似三角形的判定方法可判断△BCE∽△ACF,所以∠EBC=∠FAC=45°,然后根据三角形内角和可得∠AHB=∠ACB=45°,所以∠EHF=45°.
解答 证明:连接AC、CF,如图,
∵四边形ABCD和四边形ECGF都是正方形,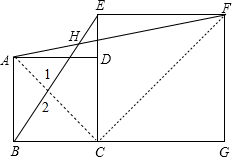
∴∠DAC=∠ACB=∠ACE=∠ECF=45°,AC=$\sqrt{2}$BC,CF=$\sqrt{2}$CE,
∴∠ACF=∠ACE+∠ECF=90°,
∵$\frac{AC}{CB}$=$\sqrt{2}$,$\frac{CF}{CE}$=$\sqrt{2}$,
∴$\frac{AC}{CB}$=$\frac{CF}{CE}$,
而∠BCE=∠ACF,
∴△BCE∽△ACF,
∴∠EBC=∠FAC=45°,
∵∠1=∠2,
∴∠AHB=∠ACB=45°,
∴∠EHF=45°.
点评 本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.解决问题的关键是构建△ACF与△BCE相似.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12. 如图所示,在△ABC中,DE∥BC,则下列比例式不成立的是( )
如图所示,在△ABC中,DE∥BC,则下列比例式不成立的是( )
 如图所示,在△ABC中,DE∥BC,则下列比例式不成立的是( )
如图所示,在△ABC中,DE∥BC,则下列比例式不成立的是( )| A. | $\frac{AD}{DB}=\frac{AE}{EC}$ | B. | $\frac{AD}{AB}=\frac{AE}{AC}$ | C. | $\frac{AD}{DB}=\frac{DE}{BC}$ | D. | $\frac{AD}{AE}=\frac{AB}{AC}$ |
19.定义:如果一元二次方程ax2+bx+c=o(a≠0)满足a-b+c=0,那么我们称这个方程为“蝴蝶”方程.已知关于x的方程ax2+bx+c=0(a≠0)是“蝴蝶”方程,且有两个相等的实数根,则下列结论中正确的是( )
| A. | b=c | B. | a=b | C. | a=c | D. | a=b=c |
16.下列关系式中,y是x的一次函数的是( )
| A. | y=x2 | B. | y=1-3x | C. | y=$\frac{1}{2x}$+2 | D. | y=$\sqrt{2}$ |
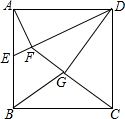 已知正方形ABCD的边长为4,取AB边上的中点E,连接DE,过点A作AF⊥DE于点F,连按CF,过点D作DG⊥CF于点G,连接BG,则BG=$\frac{4}{5}\sqrt{10}$.
已知正方形ABCD的边长为4,取AB边上的中点E,连接DE,过点A作AF⊥DE于点F,连按CF,过点D作DG⊥CF于点G,连接BG,则BG=$\frac{4}{5}\sqrt{10}$.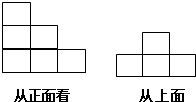 如图,是一个立体图形从两个不同方向看到的形状图,这个立体图形是由一些相同的小正方体构成,这些相同的小正方体的个数最多是( )
如图,是一个立体图形从两个不同方向看到的形状图,这个立体图形是由一些相同的小正方体构成,这些相同的小正方体的个数最多是( )