题目内容
4.小明和3个女生、4个男生玩丢手绢的游戏,如果小明随意将手绢丢在一名同学后面,那么这名同学不是女生的概率是( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{4}{7}$ | D. | $\frac{3}{7}$ |
分析 根据随机事件概率大小的求法,找准两点:
①符合条件的情况数目;
②全部情况的总数.
二者的比值就是其发生的概率的大小.
解答 解:因为小明随意将手帕丢在一名同学的后面共有7种情况,
这名同学不是女生的可能性为4种,
所以这名同学不是女生的概率是$\frac{4}{7}$;
故选C.
点评 本题考查概率的求法与运用,一般方法为:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
12. 如图所示,在△ABC中,DE∥BC,则下列比例式不成立的是( )
如图所示,在△ABC中,DE∥BC,则下列比例式不成立的是( )
 如图所示,在△ABC中,DE∥BC,则下列比例式不成立的是( )
如图所示,在△ABC中,DE∥BC,则下列比例式不成立的是( )| A. | $\frac{AD}{DB}=\frac{AE}{EC}$ | B. | $\frac{AD}{AB}=\frac{AE}{AC}$ | C. | $\frac{AD}{DB}=\frac{DE}{BC}$ | D. | $\frac{AD}{AE}=\frac{AB}{AC}$ |
19.定义:如果一元二次方程ax2+bx+c=o(a≠0)满足a-b+c=0,那么我们称这个方程为“蝴蝶”方程.已知关于x的方程ax2+bx+c=0(a≠0)是“蝴蝶”方程,且有两个相等的实数根,则下列结论中正确的是( )
| A. | b=c | B. | a=b | C. | a=c | D. | a=b=c |
16.下列关系式中,y是x的一次函数的是( )
| A. | y=x2 | B. | y=1-3x | C. | y=$\frac{1}{2x}$+2 | D. | y=$\sqrt{2}$ |
14.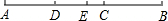 如图,点C为线段AB上一点,AC:CB=3:2,D、E两点分别为AC、AB的中点,若线段DE=2cm,则AB的长为( )
如图,点C为线段AB上一点,AC:CB=3:2,D、E两点分别为AC、AB的中点,若线段DE=2cm,则AB的长为( )
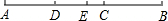 如图,点C为线段AB上一点,AC:CB=3:2,D、E两点分别为AC、AB的中点,若线段DE=2cm,则AB的长为( )
如图,点C为线段AB上一点,AC:CB=3:2,D、E两点分别为AC、AB的中点,若线段DE=2cm,则AB的长为( )| A. | 8cm | B. | 12cm | C. | 14cm | D. | 10cm |
 (1)如图1,一长方体的长、宽、高分别如图所示.(注:①、②两小题中每个小正方形的边长均为1个单位)
(1)如图1,一长方体的长、宽、高分别如图所示.(注:①、②两小题中每个小正方形的边长均为1个单位)

 如图,矩形ABCD中,AC、BD交于O点,AE平分∠BAD交BC于E点且∠AOD=120°,求∠AOE的度数.
如图,矩形ABCD中,AC、BD交于O点,AE平分∠BAD交BC于E点且∠AOD=120°,求∠AOE的度数.