题目内容
4.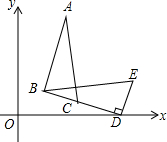 如图,在△BDE中,∠BDE=90°,BD=4$\sqrt{2}$,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转得到△ABC的位置,点C在BD上,则过A、B、D三点圆的圆心坐标为(3,2$\sqrt{3}$).
如图,在△BDE中,∠BDE=90°,BD=4$\sqrt{2}$,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转得到△ABC的位置,点C在BD上,则过A、B、D三点圆的圆心坐标为(3,2$\sqrt{3}$).
分析 作线段AB与BD的垂直平分线,它们的交点即为过A、B、D三点圆的圆心P,连接PD、PB、PE,过P作PF⊥x轴于F,利用旋转的性质得BC=DE,PB=PD,PE=PC,则可证明△PBC≌△PDE,所以∠PBC=∠PDE,易得∠PDB=∠PDE=$\frac{1}{2}$∠BDE=45°,于是可判断△PBD为等腰直角三角形,则PD=$\frac{\sqrt{2}}{2}$BD=4,然后在Rt△PDF中利用含30度的直角三角形三边的关系计算出DF和PF,从而可确定P点坐标.
解答 解:如图,作线段AB与BD的垂直平分线,它们的交点即为过A、B、D三点圆的圆心P,连接PD、PB、PE,过P作PF⊥x轴于F,
∵△BDE旋转得到△ABC的位置,点C在BD上,
∴BC=DE,PB=PD,PE=PC,
在△PBC和PDE中
$\left\{\begin{array}{l}{PB=PD}\\{BC=DE}\\{PC=PE}\end{array}\right.$,
∴△PBC≌△PDE,
∴∠PBC=∠PDE,
而PB=PD,
∴∠PBD=∠PDB,
∴∠PDB=∠PDE=$\frac{1}{2}$∠BDE=45°,
∴△PBD为等腰直角三角形,
∴PD=$\frac{\sqrt{2}}{2}$BD=4,
∵∠BDO=15°,
∴∠PDO=45°+15°=60°,
∴∠DPF=30°,
∴DF=$\frac{1}{2}$PD=$\frac{1}{2}$×4=2,PF=$\sqrt{3}$DF=2$\sqrt{3}$,
∵点D的坐标是(5,0),
∴OF=OD-DF=5-2=3,
∴P点坐标为(3,2$\sqrt{3}$).
故答案为:(3,2$\sqrt{3}$).
点评 本题考查了三角形的外接圆与外心:经过三角形的三个顶点的圆,叫做三角形的外接圆.三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.解决本题的关键是证明△PBD为等腰直角三角形.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案| 甲的成绩 | 乙的成绩 | ||||||||||
| 环数 | 6 | 7 | 8 | 9 | 10 | 环数 | 6 | 7 | 8 | 9 | 10 |
| 频数 | 3 | 5 | 4 | 5 | 3 | 频数 | 5 | 3 | 4 | 3 | 5 |
| A. | 甲 | B. | 乙 | ||
| C. | 甲、乙两人成绩稳定程度相同 | D. | 无法确定 |
 如图,已知AB∥CD,∠1=140°,则∠2=( )
如图,已知AB∥CD,∠1=140°,则∠2=( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
 已知如图在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明( )
已知如图在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明( )| A. | △ADC∽△ACB | B. | △BDC∽△BCA | C. | △ADC∽△CBD | D. | 无法判断 |
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论;①2a+b>0;②abc<0;③b2-4ac>0;④a+b+c<0;⑤4a-2b+c<0;⑥若(x1,y1)、(x2,y2)在函数图象上,当x1<x2<1时,y1<y2,其中正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论;①2a+b>0;②abc<0;③b2-4ac>0;④a+b+c<0;⑤4a-2b+c<0;⑥若(x1,y1)、(x2,y2)在函数图象上,当x1<x2<1时,y1<y2,其中正确的个数是( )