题目内容
9. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论;①2a+b>0;②abc<0;③b2-4ac>0;④a+b+c<0;⑤4a-2b+c<0;⑥若(x1,y1)、(x2,y2)在函数图象上,当x1<x2<1时,y1<y2,其中正确的个数是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论;①2a+b>0;②abc<0;③b2-4ac>0;④a+b+c<0;⑤4a-2b+c<0;⑥若(x1,y1)、(x2,y2)在函数图象上,当x1<x2<1时,y1<y2,其中正确的个数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 由二次函数的开口方向,对称轴x>1,以及二次函数与y的交点在x轴的上方,与x轴有两个交点等条件来判断各结论的正误即可.
解答 解:①∵二次函数的开口向下,∴a<0,对称轴在1的右边,∴-$\frac{b}{2a}$>1,∴2a+b>0,故①正确;
②观察图象,抛物线与y轴的交点在x轴下方,∴c<0,
又∵对称轴为x=-$\frac{b}{2a}$在x轴的正半轴上,故x=-$\frac{b}{2a}$>0,∵a<0,∴b>0.
∴abc>0,故②错误.
③∵二次函数与x轴有两个交点,∴△=b2-4ac>0,故③正确.
④观察图象,当x=1时,函数值y=a+b+c>0,故④错误;
⑤观察图象,当x=-2时,函数值y=4a-2b+c<0,故⑤正确.
⑥若(x1,y1)、(x2,y2)在函数图象上,当x1<x2<1时,y1<y2,故⑥正确.
故选:C.
点评 此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).

练习册系列答案
相关题目
17. 如图是由一水桶抽象而成的几何图形,其俯视图是( )
如图是由一水桶抽象而成的几何图形,其俯视图是( )
 如图是由一水桶抽象而成的几何图形,其俯视图是( )
如图是由一水桶抽象而成的几何图形,其俯视图是( )| A. |  | B. |  | C. |  | D. |  |
1.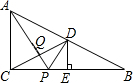 如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是( )
如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是( )
 如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是( )
如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是( )| A. | AQ=$\frac{5}{2}$PQ | B. | AQ=3PQ | C. | AQ=$\frac{8}{3}$PQ | D. | AQ=4PQ |
18.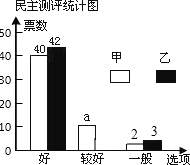 九年级一班邀请A、B、C、D、E五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投费,绘制了如下的统计表和不完整的条形统计图:
九年级一班邀请A、B、C、D、E五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投费,绘制了如下的统计表和不完整的条形统计图:
五位评委的打分表
并求得了五位评委对甲同学才艺表演所打分数的平均分和中位数:
$\overline{{x}_{甲}}$=$\frac{89+91+93+94+86}{5}$=90.6(分);中位数是91分.
(1)求五位评委对乙同学才艺表演所打分数的平均分和中位数;
(2)a=8,并补全条形统计图:
(3)为了从甲、乙二人中只选拔出一人去参加艺术节演出,班级制定了如下的选拔规则:

①当k=0.6时,通过计算说明应选拔哪位同学去参加艺术节演出?
②通过计算说明k的值不能是多少?
 九年级一班邀请A、B、C、D、E五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投费,绘制了如下的统计表和不完整的条形统计图:
九年级一班邀请A、B、C、D、E五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投费,绘制了如下的统计表和不完整的条形统计图:五位评委的打分表
| A | B | C | D | E | |
| 甲 | 89 | 91 | 93 | 94 | 86 |
| 乙 | 88 | 87 | 90 | 98 | 92 |
$\overline{{x}_{甲}}$=$\frac{89+91+93+94+86}{5}$=90.6(分);中位数是91分.
(1)求五位评委对乙同学才艺表演所打分数的平均分和中位数;
(2)a=8,并补全条形统计图:
(3)为了从甲、乙二人中只选拔出一人去参加艺术节演出,班级制定了如下的选拔规则:

①当k=0.6时,通过计算说明应选拔哪位同学去参加艺术节演出?
②通过计算说明k的值不能是多少?
 如图,在?ABCD中,BC=10,则AD的长为10.
如图,在?ABCD中,BC=10,则AD的长为10.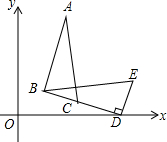 如图,在△BDE中,∠BDE=90°,BD=4$\sqrt{2}$,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转得到△ABC的位置,点C在BD上,则过A、B、D三点圆的圆心坐标为(3,2$\sqrt{3}$).
如图,在△BDE中,∠BDE=90°,BD=4$\sqrt{2}$,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转得到△ABC的位置,点C在BD上,则过A、B、D三点圆的圆心坐标为(3,2$\sqrt{3}$).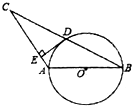 如图,⊙O的直径AB=4,sin∠ABC=$\frac{1}{2}$,BC交⊙O于D,D是BC的中点.
如图,⊙O的直径AB=4,sin∠ABC=$\frac{1}{2}$,BC交⊙O于D,D是BC的中点.