题目内容
19.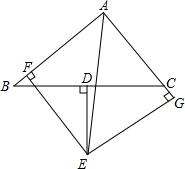 如图,在△ABC中,D为BC中点,DE⊥BC交∠BAC的平分线AE于E,EF⊥AB于F,EG⊥AC交AC的延长线于G,
如图,在△ABC中,D为BC中点,DE⊥BC交∠BAC的平分线AE于E,EF⊥AB于F,EG⊥AC交AC的延长线于G,(1)求证:BF=CG;
(2)若AB=7,AC=3,求AF的长.
分析 (1)连接EB、EC,只要证明Rt△BEF≌Rt△CEG,即可得到BF=CG.
(2)由RT△AEF≌RT△AEG得AF=AG,再由Rt△BFE≌Rt△CGE得BF=CG,易知AB+AC=2AF由此即可解决问题.
解答 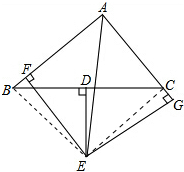 (1)证明:如图,连接BE、EC,
(1)证明:如图,连接BE、EC,
∵ED⊥BC,
D为BC中点,
∴BE=EC,
∵EF⊥AB EG⊥AG,且AE平分∠FAG,
∴FE=EG,
在Rt△BFE和Rt△CGE中,
$\left\{\begin{array}{l}{BE=CE}\\{EF=EG}\end{array}\right.$,
∴Rt△BFE≌Rt△CGE(HL),
∴BF=CG.
(2)解:在RT△AEF和RT△AEG中,
$\left\{\begin{array}{l}{AE=AE}\\{EF=EG}\end{array}\right.$,
∴RT△AEF≌RT△AEG(HL),
∴AF=AG,
∵Rt△BFE≌Rt△CGE(HL),
∴BF=CG,
∴AB+AC=AF+BF+AG-CG=2AF,
∴2AF=10,
∴AF=5.
点评 本题考查了全等三角形的判定和性质、相等垂直平分线的性质、角平分线的性质等知识,解题的关键是正确寻找全等三角形,记住这个图形基本结论AB+AC=2AF,属于中考常考题型.

练习册系列答案
相关题目
10.在实数0,-π,-4,-$\sqrt{12}$中,最小的数是( )
| A. | 0 | B. | -π | C. | -4 | D. | -$\sqrt{12}$ |
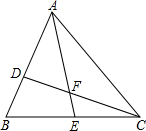 如图,点D在△ABC边AB上且AD:BD=2:1,E是BC的中点,设S1为△ADF的面积,S2为△CEF的面积.若S△ABC=24,则S1-S2=4.
如图,点D在△ABC边AB上且AD:BD=2:1,E是BC的中点,设S1为△ADF的面积,S2为△CEF的面积.若S△ABC=24,则S1-S2=4.