题目内容
4.比较大小:-$\sqrt{3}$>-$\sqrt{3.14}$
$\sqrt{10}$> $\sqrt{8}$.
分析 (1)首先分别求出-$\sqrt{3}$、-$\sqrt{3.14}$的平方的大小,然后判断出两个数的平方的大小关系,再根据实数大小比较的方法,判断出-$\sqrt{3}$、-$\sqrt{3.14}$的大小关系即可.
(2)首先分别求出$\sqrt{10}$、$\sqrt{8}$的平方的大小,然后判断出两个数的平方的大小关系,再根据实数大小比较的方法,判断出$\sqrt{10}$、$\sqrt{8}$的大小关系即可.
解答 解:${(-\sqrt{3})}^{2}$=3,${(-\sqrt{3.14})}^{2}$=3.14,
∵3<3.14,
∴-$\sqrt{3}$>-$\sqrt{3.14}$.
(2)${(\sqrt{10})}^{2}$=10,${(\sqrt{8})}^{2}$=8,
∵10>8,
∴$\sqrt{10}$>$\sqrt{8}$.
故答案为:>、>.
点评 (1)此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是要明确:正实数>0>负实数,两个负实数绝对值大的反而小.
(2)解答此题的关键还要明确比较两个数的平方的大小在实数大小比较中的应用.

练习册系列答案
相关题目
16.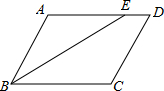 如图,在?ABCD中,BE平分∠ABC交AD于E,BC=8cm,CD=6cm,∠D=60°,则下列说法中错误的是( )
如图,在?ABCD中,BE平分∠ABC交AD于E,BC=8cm,CD=6cm,∠D=60°,则下列说法中错误的是( )
 如图,在?ABCD中,BE平分∠ABC交AD于E,BC=8cm,CD=6cm,∠D=60°,则下列说法中错误的是( )
如图,在?ABCD中,BE平分∠ABC交AD于E,BC=8cm,CD=6cm,∠D=60°,则下列说法中错误的是( )| A. | ∠C=120° | B. | AE=6cm | C. | AD=8cm | D. | ∠BED=140° |
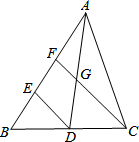 如图,在△ABC中,AD是BC边上的中线,点E、F在AB边上,且E是BF中点,连接DE,CF交AD于G,.
如图,在△ABC中,AD是BC边上的中线,点E、F在AB边上,且E是BF中点,连接DE,CF交AD于G,.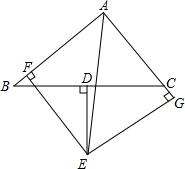 如图,在△ABC中,D为BC中点,DE⊥BC交∠BAC的平分线AE于E,EF⊥AB于F,EG⊥AC交AC的延长线于G,
如图,在△ABC中,D为BC中点,DE⊥BC交∠BAC的平分线AE于E,EF⊥AB于F,EG⊥AC交AC的延长线于G,