题目内容
1.在Rt△ABC中,∠C=90°,AB=13,AC=12,BC=5,则三个内角平分线的交点到边的距离是2.分析 设三个内角平分线的交点到边的距离是x,根据角平分线的性质和三角形的面积公式计算即可.
解答 解:设三个内角平分线的交点到边的距离是x,
由角平分线的性质可知三个内角平分线的交点到边的距离相等,
由三角形的面积公式得,$\frac{1}{2}$×12×5=$\frac{1}{2}$×12×x+$\frac{1}{2}$×13×x+$\frac{1}{2}$×x×5,
解得,x=2,
故答案为:2.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,动点P从点A开始沿AB边向B以1cm/s的速度移动(不与点B重合);动点Q从B点开始沿BC边向点C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,出发多少秒后,四边形APQC的面积为16cm2?
如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,动点P从点A开始沿AB边向B以1cm/s的速度移动(不与点B重合);动点Q从B点开始沿BC边向点C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,出发多少秒后,四边形APQC的面积为16cm2? △ABC中,∠A=30°,∠B=45°,AC=4,求AB的长?
△ABC中,∠A=30°,∠B=45°,AC=4,求AB的长?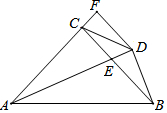 如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于 D,DF⊥AC交AC的延长线于F,连接CD,给出四个结论:
如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于 D,DF⊥AC交AC的延长线于F,连接CD,给出四个结论: