题目内容
17.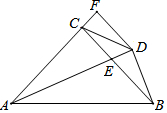 如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于 D,DF⊥AC交AC的延长线于F,连接CD,给出四个结论:
如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于 D,DF⊥AC交AC的延长线于F,连接CD,给出四个结论:①AE=2BD; ②DC=DB; ③AB-AC=CE; ④CE=2FC;
其中正确的结论有①②③④.(只需要填写序号)
分析 注意到AD具备“两种功能”:角平分线、垂线;因此,延长BD、AC交于点G,则三角形ABG就是等腰,从而AB=AG,BD=DG,四个个判断不言而喻.
解答 解:①延长BD、AC交于点G,如图1,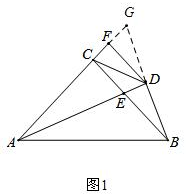
∵AD⊥BD,AD平分∠CAB,
∴∠DAG=∠DAB,
∵∠G+∠DAG=90°,∠ABD+∠DAB=90°,
∴∠G=∠ABD,
∴AG=AB,DG=DB,
∵∠BCG=90°,
∴CD=BD=DG,故②正确,
∵AC⊥BC,
∴∠CAE+∠CEA=∠DEB+∠DBE=90°,
∴∠CAE=∠DBE,
在△CAE和△CBG中,
$\left\{\begin{array}{l}{CA=CB}\\{∠ACE=∠BCG}\\{∠CAE=∠CBG}\end{array}\right.$,
∴△CAE≌△CBG(AAS),
∴AE=BG=2BD,CE=CG,故①正确;
②过点E作EH⊥AB于H,如图2,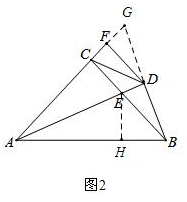
∵∠ABC=45°,
∴△BHE是等腰直角三角形,
∴EH=BH,
∵AE平分∠CAB,
∴EH=CE,
∴BH=CG,
∴AB-AC=CE,故③正确;
③如图1,
∵DF⊥AC,
∴DF∥BC,
∵BD=DG,
∴CF=FG,
∴CE=2FC,故④正确.
故答案为①②③④.
点评 本题考查了等腰直角三角形的性质、角平分线的性质、全等三角形的判定与性质、等腰三角形三线合一、中位线等知识点,难度适中.解答本题的突破口是发现AD是“三线”,如果有某条线既是角平分线又是垂线,那么以这条线为对称轴一定“隐藏”着一个等腰三角形,通过辅助线把等腰三角形暴露出来,问题往往可以迎刃而解.

练习册系列答案
相关题目
8.实数$\sqrt{6}$的值在( )
| A. | 3与4之间 | B. | 2与3之间 | C. | 1与2之间 | D. | 0与1之间 |
 如图,在平面直角坐标系中,点P的坐标为(0,8),直线y=$\frac{3}{4}$x-6与x轴、y轴分别交于点A、B,点M是直线AB上的一个动点,则PM长的最小值为$\frac{56}{5}$.
如图,在平面直角坐标系中,点P的坐标为(0,8),直线y=$\frac{3}{4}$x-6与x轴、y轴分别交于点A、B,点M是直线AB上的一个动点,则PM长的最小值为$\frac{56}{5}$.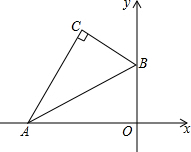 如图,在平面直角坐标系中,含30°锐角的三角板的直角顶点C落在第二象限,其斜边两端点A、B分别落在x轴、y轴上,且AB=12cm,OB=6cm.点C′是第二象限内不与点C重合的一个点,且以A、B、C′为顶点的三角形与△ABC相似(相似比不为1),则点C′的坐标为(-6$\sqrt{3}$,24)、(-2$\sqrt{3}$,12)、(-12$\sqrt{3}$,18)和(-8$\sqrt{3}$,6).
如图,在平面直角坐标系中,含30°锐角的三角板的直角顶点C落在第二象限,其斜边两端点A、B分别落在x轴、y轴上,且AB=12cm,OB=6cm.点C′是第二象限内不与点C重合的一个点,且以A、B、C′为顶点的三角形与△ABC相似(相似比不为1),则点C′的坐标为(-6$\sqrt{3}$,24)、(-2$\sqrt{3}$,12)、(-12$\sqrt{3}$,18)和(-8$\sqrt{3}$,6). 如图所示,AD∥BC,AB∥DC,M,Q分别在DA、BC的最长线上,且AM=CQ,连接MQ,分别交CD,BD,AB于点P,E,N,求证:△AMN≌△CQP.
如图所示,AD∥BC,AB∥DC,M,Q分别在DA、BC的最长线上,且AM=CQ,连接MQ,分别交CD,BD,AB于点P,E,N,求证:△AMN≌△CQP.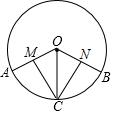 如图,OA、OB、OC是⊙O的半径,$\widehat{AC}$=$\widehat{BC}$,CM⊥OA于M,CN⊥OB于N,求证:MC=NC.
如图,OA、OB、OC是⊙O的半径,$\widehat{AC}$=$\widehat{BC}$,CM⊥OA于M,CN⊥OB于N,求证:MC=NC.