题目内容
16.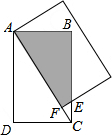 把两个相同的矩形按如图方式叠合起来,重叠部分为图中的阴影部分,已知AD=4,DC=3,则重叠部分的面积为( )
把两个相同的矩形按如图方式叠合起来,重叠部分为图中的阴影部分,已知AD=4,DC=3,则重叠部分的面积为( )| A. | 6 | B. | $\frac{16}{3}$ | C. | $\frac{21}{4}$ | D. | $\frac{45}{8}$ |
分析 根据勾股定理求出AC,继而求出CE,易证得△CEF∽△CAB,根据相似三角形的相似比等于对应高之比求出,求出S四边形ABEF=$\frac{15}{16}$S△ABC,代入求出即可.
解答 解:∵在矩形ABCD中,AD=4,DC=3,
∴在Rt△ADC中,AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=5,
∴CF=AC-CF=5-4=1,
由矩形的性质得:∠AEF=∠CBA=90°,
∵∠FAE=∠CAB,
∴△CEF∽△CAB,
∴$\frac{{S}_{△CEF}}{{S}_{△CAB}}$=($\frac{CF}{CB}$)2=$\frac{1}{16}$,
∴S四边形ABEF=$\frac{15}{16}$S△ABC=$\frac{15}{16}$×$\frac{1}{2}$×3×4=$\frac{45}{8}$,
故选D.
点评 此题考查了相似三角形的判定与性质、勾股定理以及矩形的性质.注意相似三角形的面积比等于相似比的平方.

练习册系列答案
相关题目
4.已知△ABC两边长度分别是3cm,4cm,则连结各边中点的三角形的周长可能为( )
| A. | 3.5cm | B. | 12cm | C. | 6.4cm | D. | 10cm |
8.方程3x2=0和方程5x2=6x的根( )
| A. | 都是x=0 | B. | 有一个相同,x=0 | C. | 都不相同 | D. | 以上都不正确 |
6.若点M(-2,y1),N(-1,y2),P(8,y3)在抛物线y=-x2+2x上,则下列结论正确的( )
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y1<y2 | D. | y1<y3<y2 |