题目内容
6.某商场将进价为2000元的冰箱以3000元售出,平均每天能售出8台,为配合国家“家电下乡”政策实施,商场决定在保证盈利的前提下采取适当的降价措施.调查表明:如果这种冰箱每台的降价不超过500元时.这种冰箱的售价每降低50元,平均每天就能多售出4台;如果这种冰箱每台的降价超过500元后,若再降价,每降低50元,平均每天就能多售出10台.设这种冰箱每台降价x元(x为50的整数倍),每天的销售量为y件.(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)设商场每天的销售利润为W元,请直按写出W与x的函数关系式;
(3)当这种冰箱每台的售价定为多少元时,每天可获得最大利润?最大利润是多少元?
分析 (1)分两种情况:每台的降价不超过500元时,每台的降价超过500元后,由题意直接得出y与x的函数关系式即可;
(2)用每一台冰箱的利润乘以一天销售台数,整理即可得解;
(3)利用配方法根据(2)中的关系式求得答案即可.
解答 解:(1)当x≤500时,y=8+$\frac{x}{50}$×4=$\frac{2}{25}$x+8;
当500<x≤1000时,y=8+$\frac{x}{50}$×10=$\frac{1}{5}$x+8;
(2)由题意得:
当x≤500时,W=($\frac{2}{25}$x+8)(1000-x)=-$\frac{2}{25}$x2+72x+8000;
当500<x≤1000时,W=($\frac{1}{5}$x+8)(1000-x)=-$\frac{1}{5}$x2+192x+8000;
(3)当x≤500时,W=-$\frac{2}{25}$x2+72x+8000=-$\frac{2}{25}$(x-450)2+24200;
当x=450时,W=24200,
当500<x≤1000时,W=-$\frac{1}{5}$x2+192x+8000=-$\frac{1}{5}$(x-480)2+10880;
当x=480时,W=10880,(不合题意),
所以当x=450时,W最大=24200元.
点评 此题主要考查了二次函数的应用以及二次函数的最值问题,根据每天的利润=一件的利润×销售量,建立函数关系式,借助二次函数解决实际问题是解题关键.

练习册系列答案
相关题目
14.一水果商为了获得更多利润,对往年销售某水果情况进行了统计,得到如表的数据:
(1)已知y是x的一次函数,请同学们根据表中数据求出y与x之间的函数关系式;
(2)若该水果进价为13元/千克,设销售利润为W(元);试求销售利润W(元)与销售价x(元/千克)之间的函数关系式,求当x取何值时,销售利润最大?
| 销售价x(元/千克) | … | 25 | 24 | 23 | 22 | … |
| 销售量y(千克) | … | 2000 | 2500 | 3000 | 3500 | … |
(2)若该水果进价为13元/千克,设销售利润为W(元);试求销售利润W(元)与销售价x(元/千克)之间的函数关系式,求当x取何值时,销售利润最大?
15.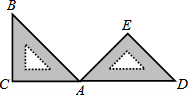 如图,将含45°的直角三角板ABC绕着点A顺时针旋转到△ADE处(点C,A,D在一条直线上),则这次旋转的旋转角为( )
如图,将含45°的直角三角板ABC绕着点A顺时针旋转到△ADE处(点C,A,D在一条直线上),则这次旋转的旋转角为( )
 如图,将含45°的直角三角板ABC绕着点A顺时针旋转到△ADE处(点C,A,D在一条直线上),则这次旋转的旋转角为( )
如图,将含45°的直角三角板ABC绕着点A顺时针旋转到△ADE处(点C,A,D在一条直线上),则这次旋转的旋转角为( )| A. | 45° | B. | 90° | C. | 135° | D. | 180° |
16.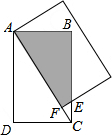 把两个相同的矩形按如图方式叠合起来,重叠部分为图中的阴影部分,已知AD=4,DC=3,则重叠部分的面积为( )
把两个相同的矩形按如图方式叠合起来,重叠部分为图中的阴影部分,已知AD=4,DC=3,则重叠部分的面积为( )
 把两个相同的矩形按如图方式叠合起来,重叠部分为图中的阴影部分,已知AD=4,DC=3,则重叠部分的面积为( )
把两个相同的矩形按如图方式叠合起来,重叠部分为图中的阴影部分,已知AD=4,DC=3,则重叠部分的面积为( )| A. | 6 | B. | $\frac{16}{3}$ | C. | $\frac{21}{4}$ | D. | $\frac{45}{8}$ |
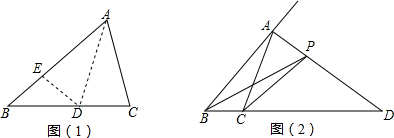
 如图,在等边△ABC中,BD=CE,AD与BE相交于点P,则∠BPD=60°.
如图,在等边△ABC中,BD=CE,AD与BE相交于点P,则∠BPD=60°.