题目内容
5.已知关于x的方程x2-(2k+1)x+k2+1=0.(1)当k取何值时,方程有实数根?
(2)当k取何值时,方程没有实数根?
分析 (1)由关于x的方程x2-(2k+1)x+k2+1=0有实数根,可得△≥0,继而求得k的取值;
(2)由关于x的方程x2-(2k+1)x+k2+1=0没有实数根,可得△<0,继而求得答案.
解答 解:(1)∵方程有实数根,
∴△=[-(2k+1)]2-4(k2+1)=4k-3≥0.
解得:k≥$\frac{3}{4}$,
∴当k≥$\frac{3}{4}$时,方程有实数根;
(2)∵方程没有实数根,
∴△=4k-3<0,
解得:k<$\frac{3}{4}$,
∴当k<$\frac{3}{4}$时,方程没有实数根.
点评 此题考查了根的判别式.注意△>0?方程有两个不相等的实数根;△=0?方程有两个相等的实数根;△<0?方程没有实数根.

练习册系列答案
相关题目
15.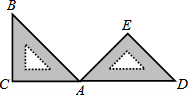 如图,将含45°的直角三角板ABC绕着点A顺时针旋转到△ADE处(点C,A,D在一条直线上),则这次旋转的旋转角为( )
如图,将含45°的直角三角板ABC绕着点A顺时针旋转到△ADE处(点C,A,D在一条直线上),则这次旋转的旋转角为( )
 如图,将含45°的直角三角板ABC绕着点A顺时针旋转到△ADE处(点C,A,D在一条直线上),则这次旋转的旋转角为( )
如图,将含45°的直角三角板ABC绕着点A顺时针旋转到△ADE处(点C,A,D在一条直线上),则这次旋转的旋转角为( )| A. | 45° | B. | 90° | C. | 135° | D. | 180° |
16.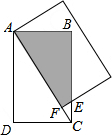 把两个相同的矩形按如图方式叠合起来,重叠部分为图中的阴影部分,已知AD=4,DC=3,则重叠部分的面积为( )
把两个相同的矩形按如图方式叠合起来,重叠部分为图中的阴影部分,已知AD=4,DC=3,则重叠部分的面积为( )
 把两个相同的矩形按如图方式叠合起来,重叠部分为图中的阴影部分,已知AD=4,DC=3,则重叠部分的面积为( )
把两个相同的矩形按如图方式叠合起来,重叠部分为图中的阴影部分,已知AD=4,DC=3,则重叠部分的面积为( )| A. | 6 | B. | $\frac{16}{3}$ | C. | $\frac{21}{4}$ | D. | $\frac{45}{8}$ |
20.下列运算中,正确的是( )
| A. | ($\sqrt{2}$+1)($\sqrt{2}$-1)=3 | B. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{2}$ | C. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | D. | 2$\sqrt{3}$+3$\sqrt{3}$=6$\sqrt{3}$ |
10.在学习了“25.1.2”概率后,平平和安安两位同学做掷质地均匀的正方体骰子试验,它们共做了120次试验,试验的结果如下表:
综合上表,平平说:“如果投掷600次,那么向上一面点数是6的次数正好是100次.”安安说:“一次实验中向上一面点数是5的概率最大”.你认为平平和安安的说法中正确的是( )
| 向上一面的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现的次数 | 14 | 18 | 12 | 16 | 40 | 20 |
| A. | 平平 | B. | 安安 | C. | 都正确 | D. | 都错误 |
15.解关于x的分式方程$\frac{1}{x-1}$+1=$\frac{m}{1-x}$时会产生增根,则m的值( )
| A. | m=1 | B. | m=-1 | C. | m=0 | D. | m=±1 |