题目内容
7.小米将两块相同的三角板摆成如图1的形状,三角板的斜边长为10cm,较小锐角为30°,点B、C、F、D在同一条直线上,且点C与点F重合,小米在对这两块三角板进行如下操作时遇到了如下问题,请你帮助他解决.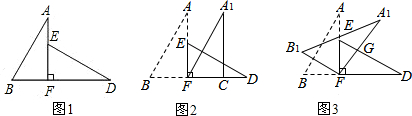
(1)将图1中的△ABC沿BD向右平移到图2的位置,使点B与点C重合,求出平移的距离;
(2)将图1中的△ABC绕点C顺时针方向旋转30°到图3的位置,A、C交DE于点G,求出线段GC的长.
分析 (1)图形平移的距离就是线段BC的长,在直角△ABC中,利用直角三角形的性质即可求解;
(2)根据旋转的性质证明∠CGD=90°,然后根据直角三角形的性质解答.
解答 解:(1)图形平移的距离就是线段BC的长.
∵直角△ABC中,AB=10cm,∠BAC=30°,
∴BC=5cm.
即平移的距离是5cm;
(2)∵∠A1CA=30°,
∴∠GCD=60°,∠D=30°,
∴∠CGD=90°,
∴在直角△ECD中,ED=10cm,EC=BC=5cm,
∴CD=5$\sqrt{3}$(cm),
∴GC=$\frac{5\sqrt{3}}{2}$(cm).
点评 本题考查了旋转的性质,正确确定旋转角,证明∠CGD=90°是本题的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
15.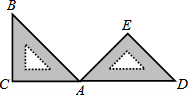 如图,将含45°的直角三角板ABC绕着点A顺时针旋转到△ADE处(点C,A,D在一条直线上),则这次旋转的旋转角为( )
如图,将含45°的直角三角板ABC绕着点A顺时针旋转到△ADE处(点C,A,D在一条直线上),则这次旋转的旋转角为( )
 如图,将含45°的直角三角板ABC绕着点A顺时针旋转到△ADE处(点C,A,D在一条直线上),则这次旋转的旋转角为( )
如图,将含45°的直角三角板ABC绕着点A顺时针旋转到△ADE处(点C,A,D在一条直线上),则这次旋转的旋转角为( )| A. | 45° | B. | 90° | C. | 135° | D. | 180° |
2. 如图,已知△ABC中,∠C=90°,AC=BC=2$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,则C′B的长为( )
如图,已知△ABC中,∠C=90°,AC=BC=2$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,则C′B的长为( )
 如图,已知△ABC中,∠C=90°,AC=BC=2$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,则C′B的长为( )
如图,已知△ABC中,∠C=90°,AC=BC=2$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,则C′B的长为( )| A. | 2$\sqrt{3}$-2 | B. | $\sqrt{3}$ | C. | 4-2$\sqrt{2}$ | D. | 2 |
16.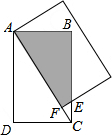 把两个相同的矩形按如图方式叠合起来,重叠部分为图中的阴影部分,已知AD=4,DC=3,则重叠部分的面积为( )
把两个相同的矩形按如图方式叠合起来,重叠部分为图中的阴影部分,已知AD=4,DC=3,则重叠部分的面积为( )
 把两个相同的矩形按如图方式叠合起来,重叠部分为图中的阴影部分,已知AD=4,DC=3,则重叠部分的面积为( )
把两个相同的矩形按如图方式叠合起来,重叠部分为图中的阴影部分,已知AD=4,DC=3,则重叠部分的面积为( )| A. | 6 | B. | $\frac{16}{3}$ | C. | $\frac{21}{4}$ | D. | $\frac{45}{8}$ |
 ,剩下的工程由乙队单独做,也正好如期完工.一同学设规定的工期为x天,根据题意列出方程:
,剩下的工程由乙队单独做,也正好如期完工.一同学设规定的工期为x天,根据题意列出方程: