题目内容
1.阅读下列材料,然后回答问题.在进行二次根式的化简与运算时,我们有时会碰上如$\frac{3}{\sqrt{5}}$,$\sqrt{\frac{2}{3}}$,$\frac{2}{\sqrt{3}+1}$一样的式子,其实我们还可以将其进一步化简:$\frac{3}{\sqrt{5}}$=$\frac{3×\sqrt{5}}{\sqrt{5}×\sqrt{5}}$=$\frac{3\sqrt{5}}{5}$;(一)
$\sqrt{\frac{2}{3}}$=$\sqrt{\frac{2×3}{3×3}}$=$\frac{\sqrt{6}}{3}$(二)
$\frac{2}{\sqrt{3}+1}$=$\frac{2×(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)}$=$\frac{2(\sqrt{3}-1)}{(\sqrt{3})^{2}-{1}^{2}}$=$\sqrt{3}$-1(三)
以上这种化简的步骤叫做分母有理化.
化简:$\frac{1}{{1+\sqrt{3}}}+\frac{1}{{\sqrt{3}+\sqrt{5}}}+\frac{1}{{\sqrt{5}+\sqrt{7}}}+…\frac{1}{{\sqrt{2n-1}+\sqrt{2n+1}}}$.
分析 原式各项分母有理化,计算即可得到结果.
解答 解:原式=$\frac{\sqrt{3}-1}{(\sqrt{3}+1)(\sqrt{3}-1)}$+$\frac{\sqrt{5}-\sqrt{3}}{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}$+…+$\frac{\sqrt{2n+1}-\sqrt{2n-1}}{(\sqrt{2n+1}+\sqrt{2n-1})(\sqrt{2n+1}-\sqrt{2n-1})}$
=$\frac{1}{2}$($\sqrt{3}$-1+$\sqrt{5}$-$\sqrt{3}$+…+$\sqrt{2n+1}$-$\sqrt{2n-1}$)
=$\frac{1}{2}$($\sqrt{2n+1}$-1).
点评 此题考查了分母有理化,找出各项的有理化因式是解本题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
9.不等式1-2x≤5的解集在数轴上表示为( )
| A. |  | B. |  | C. |  | D. | 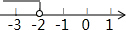 |
11.一根圆锥的主视图是等边三角形,边长为2,则这个圆锥的表面积为( )
| A. | 2π | B. | 3π | C. | $2\sqrt{3}$π | D. | $(1+2\sqrt{3}$)π |
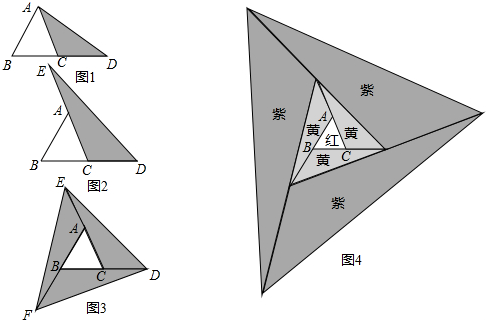
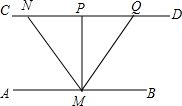 请你将下面的证明补充完整,并在括号内填写推理依据.
请你将下面的证明补充完整,并在括号内填写推理依据. 如图,点P沿半圆弧AB从A向B匀速运动,若运动时间为t,扇形OAP的面积为s,则s与t的函数图象大致是( )
如图,点P沿半圆弧AB从A向B匀速运动,若运动时间为t,扇形OAP的面积为s,则s与t的函数图象大致是( )



