题目内容
10.用正方形硬纸板做三棱柱盒子,如图,每个盒子由3个长方形侧面和2个三边均相等的三角形底面组成,硬纸板以如图2两种方法裁剪(裁剪后边角料不再利用),现有19张硬纸板,裁剪时x张用了A方法,其余用B方法.(1)用含x的式子分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?

分析 (1)由x张用A方法,就有(19-x)张用B方法,就可以分别表示出侧面个数和底面个数;
(2)根据裁剪出的侧面和底面恰好全部用完得出方程,解方程求出x的值,求出侧面的总数就可以求出结论.
解答 解:(1)∵裁剪时x张用了A方法,
∴裁剪时(19-x)张用了B方法.
∴侧面的个数为:6x+4(19-x)=(2x+76)个,
底面的个数为:5(19-x)=(95-5x)个;
(2)由题意,得
3(95-5x)=2(2x+76),
解得:x=7,
则盒子的个数为:(2x+76)÷3=30.
答:裁剪出的侧面和底面恰好全部用完,能做30个盒子.
点评 本题考查了列一元一次方程解实际问题的运用,一元一次方程的解法的运用,列代数式的运用,解答时根据裁剪出的侧面和底面个数相等建立方程是关键.

练习册系列答案
相关题目
20.下列关系式中,正确的是( )
| A. | (a+b)2=a2-2ab+b2 | B. | (a-b)2=a2-b2 | C. | (a+b)2=a2+b2 | D. | (a+b)(a-b)=a2-b2 |
18.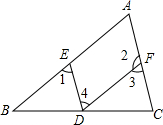 如图,在下列给出的条件下,不能判定AB∥DF的是( )
如图,在下列给出的条件下,不能判定AB∥DF的是( )
 如图,在下列给出的条件下,不能判定AB∥DF的是( )
如图,在下列给出的条件下,不能判定AB∥DF的是( )| A. | ∠A+∠2=180° | B. | ∠A=∠3 | C. | ∠1=∠4 | D. | ∠1=∠A |
15.$\sqrt{16}$=( )
| A. | ±2 | B. | 2 | C. | ±4 | D. | 4 |
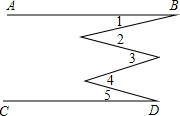 如图,AB∥CD,则∠1-∠2+∠3-∠4+∠5的数为0°.
如图,AB∥CD,则∠1-∠2+∠3-∠4+∠5的数为0°.
 如图,正方体的棱长为5,一只蚂蚁如果要沿着正方体的表面从点A爬到点B,需要爬行的最短距离是5$\sqrt{5}$.
如图,正方体的棱长为5,一只蚂蚁如果要沿着正方体的表面从点A爬到点B,需要爬行的最短距离是5$\sqrt{5}$.