题目内容
12. 请你将下面的证明补充完整,并在括号内填写推理依据.
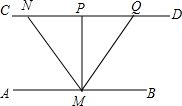
请你将下面的证明补充完整,并在括号内填写推理依据.如图,点M在直线AB上,MP⊥直线CD,垂足为P,MP平分∠NMQ,∠AMN=∠BMQ.求证:AB∥CD.
证明:∵MP平分∠NMQ,
∴∠NMP=∠PMQ(角平分线的定义)
∵∠AMN=∠BMQ;∠NMP=∠PMQ,
∴∠AMN+∠NMP=∠BMQ+∠PMQ.
∵∠AMB=180°,
∴∠AMP=90°,
∵MP⊥直线CD,
∴∠MPD=90°(垂直的定义).
∴AB∥CD(内错角相等,两直线平行)
分析 先根据角平分线的定义得出∠NMP=∠PMQ,再由∠AMN=∠BMQ得出∠AMN+∠NMP=∠BMQ+∠PMQ,根据补角的定义得出∠AMP=90°,由此可得出结论.
解答 证明:∵MP平分∠NMQ,
∴∠NMP=∠PMQ(角平分线的定义).
∵∠AMN=∠BMQ;∠NMP=∠PMQ,
∴∠AMN+∠NMP=∠BMQ+∠PMQ.
∵∠AMB=180°,
∴∠AMP=90°,
∵MP⊥直线CD,
∴∠MPD=90°(垂直的定义),
∴AB∥CD(内错角相等,两直线平行).
故答案为:角平分线的定义;∠NMP,∠BMQ;垂直的定义;内错角相等,两直线平行.
点评 本题考查的是平行线的判定,用到的知识点为:内错角相等,两直线平行.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
2.盐城市2015年初中毕业生人数达10.1万.数据10.1万用科学记数法表示为( )
| A. | 1.01×10 | B. | 10.1×104 | C. | 1.01×105 | D. | 0.101×106 |
20.下列关系式中,正确的是( )
| A. | (a+b)2=a2-2ab+b2 | B. | (a-b)2=a2-b2 | C. | (a+b)2=a2+b2 | D. | (a+b)(a-b)=a2-b2 |
17.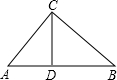 如图,在Rt△ABC中,∠ACB=90°,AB=$\sqrt{13}$,BC=2,则这个直角三角形的面积为( )
如图,在Rt△ABC中,∠ACB=90°,AB=$\sqrt{13}$,BC=2,则这个直角三角形的面积为( )
 如图,在Rt△ABC中,∠ACB=90°,AB=$\sqrt{13}$,BC=2,则这个直角三角形的面积为( )
如图,在Rt△ABC中,∠ACB=90°,AB=$\sqrt{13}$,BC=2,则这个直角三角形的面积为( )| A. | 3 | B. | 6 | C. | $\sqrt{13}$ | D. | $\frac{1}{2}$$\sqrt{13}$ |
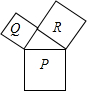 如图,分别以直角三角形的边长为边向外作正方形P、Q、R,若正方形P、Q的面积分别是4、1,则正方形R的边长是$\sqrt{3}$.
如图,分别以直角三角形的边长为边向外作正方形P、Q、R,若正方形P、Q的面积分别是4、1,则正方形R的边长是$\sqrt{3}$.