题目内容
6. 如图,点P沿半圆弧AB从A向B匀速运动,若运动时间为t,扇形OAP的面积为s,则s与t的函数图象大致是( )
如图,点P沿半圆弧AB从A向B匀速运动,若运动时间为t,扇形OAP的面积为s,则s与t的函数图象大致是( )| A. |  | B. |  | C. |  | D. |  |
分析 根据题意可以写出s与t的函数函数解析式,从而可以得到s与t的函数图象,本题得以解决.
解答 解:由题意可得,设半圆的半径为r,
$S=\frac{1}{2}t×r$,(t≥0)
即s与t的函数图象是射线,
故选C.
点评 本题考查动点问题的函数图象,解题的关键是明确题意,写出相应的函数解析式,知道相应的函数图象是什么.

练习册系列答案
相关题目
16.下列计算正确的是( )
| A. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | B. | $\sqrt{12}$÷$\sqrt{3}$=2 | C. | $\sqrt{6}$×(-$\sqrt{3}$)=3$\sqrt{2}$ | D. | ($\sqrt{3}$-1)2=2 |
17.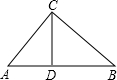 如图,在Rt△ABC中,∠ACB=90°,AB=$\sqrt{13}$,BC=2,则这个直角三角形的面积为( )
如图,在Rt△ABC中,∠ACB=90°,AB=$\sqrt{13}$,BC=2,则这个直角三角形的面积为( )
 如图,在Rt△ABC中,∠ACB=90°,AB=$\sqrt{13}$,BC=2,则这个直角三角形的面积为( )
如图,在Rt△ABC中,∠ACB=90°,AB=$\sqrt{13}$,BC=2,则这个直角三角形的面积为( )| A. | 3 | B. | 6 | C. | $\sqrt{13}$ | D. | $\frac{1}{2}$$\sqrt{13}$ |
14.下列各式中,有意义的是( )
| A. | $\sqrt{\frac{1}{9}-1}$ | B. | $\sqrt{-2}$ | C. | $-\sqrt{{{({-6})}^3}}$ | D. | $\sqrt{{{({-3})}^2}}$ |
18.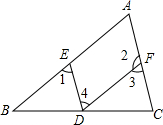 如图,在下列给出的条件下,不能判定AB∥DF的是( )
如图,在下列给出的条件下,不能判定AB∥DF的是( )
 如图,在下列给出的条件下,不能判定AB∥DF的是( )
如图,在下列给出的条件下,不能判定AB∥DF的是( )| A. | ∠A+∠2=180° | B. | ∠A=∠3 | C. | ∠1=∠4 | D. | ∠1=∠A |
15.$\sqrt{16}$=( )
| A. | ±2 | B. | 2 | C. | ±4 | D. | 4 |
 如图,四边形ABCD中,∠A=∠C=90°,BF、DE分别平分∠ABC、∠ADC.判断BF、DE是否平行,并说明理由.
如图,四边形ABCD中,∠A=∠C=90°,BF、DE分别平分∠ABC、∠ADC.判断BF、DE是否平行,并说明理由.