题目内容
14.已知:在平面直角坐标系中,点A、B坐标分别为A(-4,0)、B(2,3),AB与y轴相交于点C,点D、E分别在x、y轴上,且S△BCD=4,∠CEA=∠CBE.求:(1)点D的坐标;
(2)点E的坐标.
分析 (1)作DH⊥AB垂足为H,设点D(m,O),由△COA∽△DHA得$\frac{CO}{DH}=\frac{AC}{AD}$求出DH=$\frac{(4+m)\sqrt{5}}{5}$,根据三角形面积公式列出方程解方程即可.
(2)证明△ACE∽△AEB得$\frac{AC}{AE}=\frac{AE}{AB}$即AE2=AC•AB,求出AE,再求出OE即可解决,注意有两种情形.
解答 解:(1)如图所示,作DH⊥AB垂足为H,设点D(m,O),
∵∠CAO=∠DAH,∠COA=∠DHA=90°,
∴△COA∽△DHA,
∴$\frac{CO}{DH}=\frac{AC}{AD}$,
∵AC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,CO=2,AD=4+m
∴DH=|$\frac{(4+m)\sqrt{5}}{5}$|,
∵BC=$\sqrt{{1}^{1}+{2}^{2}}$=$\sqrt{5}$,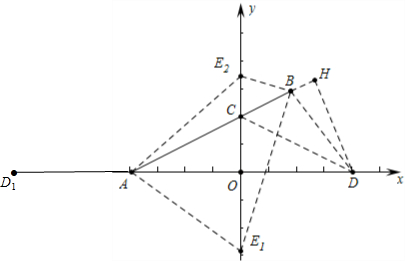
∴S△BCD=$\frac{1}{2}$•$\sqrt{5}$•|$\frac{(4+m)\sqrt{5}}{5}$|=4,
∴m=4或-12
∴点D坐标为(4,0)或(-12,0).
(2)设点E(0,n)
∵∠CAE=∠EAB,∠CEA=∠ABE,
∴△ACE∽△AEB,
∴$\frac{AC}{AE}=\frac{AE}{AB}$,
∴AE2=AC•AB,
∵AC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,AB=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$,
∴AE2=2$\sqrt{5}$×3$\sqrt{5}$=30,
∵AE>0,
∴AE=$\sqrt{30}$,
当点E1在y轴的负半轴上时,OE1=$\sqrt{30-16}$=$\sqrt{14}$,
∴点E1坐标为(0,-$\sqrt{14}$),
当E2在y轴的正半轴上时,OE2=$\sqrt{30-16}$=$\sqrt{14}$,
∴点E2坐标为(0,$\sqrt{14}$).
点评 本题考查坐标与图形的性质、勾股定理、相似三角形的判定和性质等知识,解题的关键是求面积时必须作出高DH,第二个问题关键是利用相似三角形列出比例式求出线段AE的长,属于中考常考题型.

 阅读快车系列答案
阅读快车系列答案| A. | 当x≥2时,y随x增大而增大 | B. | 对称轴为直线x=3 | ||
| C. | 当x=3时,y有最小值2 | D. | 顶点坐标为(3,2) |
| A. | 1.8(1+x)=5 | B. | 1.8(1+2x)=5 | ||
| C. | 1.8(1+x)2=5 | D. | 1.8(1+x)+1.8(1+x)2=5 |
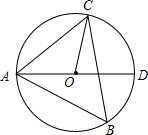 如图,△ABC内接于⊙O,AD是直径,sinB=$\frac{5}{34}$$\sqrt{34}$.
如图,△ABC内接于⊙O,AD是直径,sinB=$\frac{5}{34}$$\sqrt{34}$.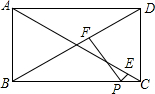 如图,矩形ABCD中,点P在BC边上,PE⊥AC,PF⊥BD,AB=6,BC=8,运用上述结论,求PE+PF的值.
如图,矩形ABCD中,点P在BC边上,PE⊥AC,PF⊥BD,AB=6,BC=8,运用上述结论,求PE+PF的值.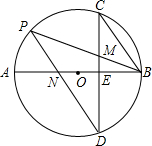 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,连接PB,PD分别交CD于M,交AB于点N,且CM=BM,
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,连接PB,PD分别交CD于M,交AB于点N,且CM=BM,