题目内容
5.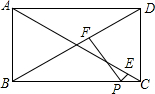 如图,矩形ABCD中,点P在BC边上,PE⊥AC,PF⊥BD,AB=6,BC=8,运用上述结论,求PE+PF的值.
如图,矩形ABCD中,点P在BC边上,PE⊥AC,PF⊥BD,AB=6,BC=8,运用上述结论,求PE+PF的值.
分析 首先连接OP.由矩形ABCD的两边AB=6,BC=8,可求得OB=OC=5,S△AOD=$\frac{1}{4}$S矩形ABCD=12,然后由S△BOC=S△BOP+S△COP=$\frac{1}{2}$OB(PE+PF)=12,即可求得答案.
解答 解:连接OP,如图所示: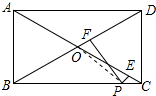
∵矩形ABCD的两边AB=6,BC=8,
∴S矩形ABCD=AB•BC=48,OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,AC=BD,∠ABC=90°,
∴OB=OC=$\frac{1}{2}$AC,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10,
∴S△BOC=$\frac{1}{4}$矩形ABCD=12,OB=OC=5,
∴S△BOC=S△BOP+S△COP=$\frac{1}{2}$OB•PE+$\frac{1}{2}$OC•PF=$\frac{1}{2}$OB(PE+PF)=$\frac{1}{2}$×5×(PE+PF)=12,
∴PE+PF=$\frac{24}{5}$.
点评 此题考查了矩形的性质、勾股定理、三角形面积的计算.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
20.若x=2m+1,y=3+4m,则用含x的代数式表示y为( )
| A. | 3+$\frac{x}{2}$ | B. | 3+x2 | C. | 3+$\frac{{x}^{2}}{4}$ | D. | 3+4x2 |
19.下列各组数的大小正确的是( )
| A. | -$\frac{2}{3}$<-$\frac{3}{5}$ | B. | -1.5>-1.4 | C. | -(-$\frac{13}{6}$)<-(-$\frac{1}{15}$) | D. | 3<-1 |