题目内容
3.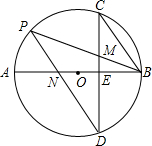 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,连接PB,PD分别交CD于M,交AB于点N,且CM=BM,
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,连接PB,PD分别交CD于M,交AB于点N,且CM=BM,(1)求证:CB∥PD;
(2)若BC=5,sin∠BPD=$\frac{3}{5}$,求⊙O的直径.
分析 (1)由等腰三角形的性质和圆周角定理得出∠P=∠C,然后根据平行线的判定定理即可得到结论;
(2)连接AC,根据垂径定理及圆周角定理得到∠P=∠A,∠ACB=90°,则sinA=sinP,然后根据正弦的定义得到=$\frac{BC}{AB}$=$\frac{3}{5}$,得出AB的长即可.
解答 (1)证明:∵CM=BM,
∴∠C=∠CBM,
∵∠C=∠P,
∴∠P=∠CBM,
∴CB∥PD;
(2)解:连接AC,如图所示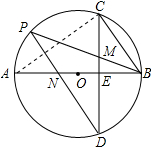
∵AB是⊙O的直径,弦CD⊥AB于点E,
∴$\widehat{BC}=\widehat{BD}$,
∴∠BPD=∠A,
∴sinA=sin∠BPD=$\frac{3}{5}$,
又∵AB为直径,
∴∠ACB=90°,
∴sinA=$\frac{BC}{AB}$=$\frac{3}{5}$,即$\frac{5}{AB}$=$\frac{3}{5}$,
解得:AB=$\frac{25}{3}$,
即⊙O的直径为$\frac{25}{3}$.
点评 本题考查了圆的综合题:在同圆或等圆中,相等的弧所对的圆周角相等,直径所对的圆周角为直角;垂直于弦的直径平分弦,并且平分弦所对的弧;运用相似三角形的判定与性质证明线段之间的关系;运用正弦的定义进行几何计算.

练习册系列答案
相关题目
 如图,在△ABE中,AB=AE,AD=AC,∠BAD=∠EAC,BC,DE交于点O,求证:∠OBE=∠OEB.
如图,在△ABE中,AB=AE,AD=AC,∠BAD=∠EAC,BC,DE交于点O,求证:∠OBE=∠OEB.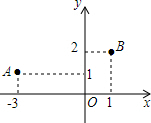 如图,在平面直角坐标系中点A(-3,1),点B(1,2),一束光线从点A处沿直线射出经x轴反射后,正好经过点B,则光线从A到B所经过路程为5.
如图,在平面直角坐标系中点A(-3,1),点B(1,2),一束光线从点A处沿直线射出经x轴反射后,正好经过点B,则光线从A到B所经过路程为5.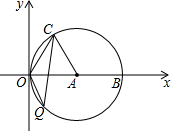 如图,在平面直角坐标系xOy中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与x轴交于O,B两点,OC为弦,∠AOC=60°,当点P在直径OB上运动时,连CP并延长与⊙A相交于点Q,PO=2或2+2$\sqrt{3}$时,△OCQ是等腰三角形.
如图,在平面直角坐标系xOy中,点A的坐标为(4,0),以点A为圆心,4为半径的圆与x轴交于O,B两点,OC为弦,∠AOC=60°,当点P在直径OB上运动时,连CP并延长与⊙A相交于点Q,PO=2或2+2$\sqrt{3}$时,△OCQ是等腰三角形. 如图,在Rt△ABC中,∠BAC的平分线交BC于点D,E为AB上一点,DE=DC,以D为圆心,DB为半径作⊙D.求证:
如图,在Rt△ABC中,∠BAC的平分线交BC于点D,E为AB上一点,DE=DC,以D为圆心,DB为半径作⊙D.求证: