题目内容
10．对于y=（x-3）2+2的图象下列叙述错误的是（ ）| A． | 当x≥2时，y随x增大而增大 | B． | 对称轴为直线x=3 | ||
| C． | 当x=3时，y有最小值2 | D． | 顶点坐标为（3，2） |
分析 根据二次函数的性质，结合顶点坐标，即可得出二次函数的顶点坐标以及对称轴和增减性，分别分析即可．
解答 解：由y=（x-3）2+2可知：顶点坐标为（3，2），对称轴为x=3，故B、D正确；
因为a=1＞0，所以开口向上，当x=3时，y有最小值2，当x＞3时，y随x增大而增大，故C正确，A错误；
故选A．
点评 本题考查了二次函数的性质，主要利用了开口方向，顶点坐标，对称轴以及二次函数的增减性．
练习册系列答案
相关题目
5．如果10b=n，那么称b为n的劳格数，记为b=d（n），如102=100，则2=d（100）；104=10000，则4=d（10000）．由定义可知：10b=n与b=d（n）所表示的是b，n两个量之间的同一关系．
（1）根据劳格数的定义，填空：d（10）=1，d（103）=3；
（2）劳格数有如下运算性质：若m，n为正数，则d（mn）=d（m）+d（n），d（$\frac{m}{n}$）=d（m）-d（n）．
根据运算性质填空，填空：若d（2）=0.3010，则d（4）=0.6020；d（5）=0.6990；d（0.08）=-1.0970．
（3）下表中与数x对应的劳格数d（x）有且只有两个是错误的，请找出错误的劳格数，说明理由并改正．
（1）根据劳格数的定义，填空：d（10）=1，d（103）=3；
（2）劳格数有如下运算性质：若m，n为正数，则d（mn）=d（m）+d（n），d（$\frac{m}{n}$）=d（m）-d（n）．
根据运算性质填空，填空：若d（2）=0.3010，则d（4）=0.6020；d（5）=0.6990；d（0.08）=-1.0970．
（3）下表中与数x对应的劳格数d（x）有且只有两个是错误的，请找出错误的劳格数，说明理由并改正．
| x | 1.5 | 3 | 5 | 6 | 8 | 9 | 12 | 27 |
| d（x） | 3a-b+c | 2a-b | a+c | 1+a-b-c | 3-3a-3c | 4a-2b | 3-b-2c | 6a-3b |
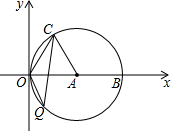如图，在平面直角坐标系xOy中，点A的坐标为（4，0），以点A为圆心，4为半径的圆与x轴交于O，B两点，OC为弦，∠AOC=60°，当点P在直径OB上运动时，连CP并延长与⊙A相交于点Q，PO=2或2+2$\sqrt{3}$时，△OCQ是等腰三角形．
19．下列各组数的大小正确的是（ ）
| A． | -$\frac{2}{3}$＜-$\frac{3}{5}$ | B． | -1.5＞-1.4 | C． | -（-$\frac{13}{6}$）＜-（-$\frac{1}{15}$） | D． | 3＜-1 |