Question

4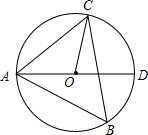．如图，△ABC内接于⊙O，AD是直径，sinB=$\frac{5}{34}$$\sqrt{34}$．
（1）求AD：AC的值；
（2）若△AOC的面积为15，求AD的长．

Answer 1

分析 （1）连接CD，根据圆周角定理得出∠ACD=90°，∠ADC=∠B，根据sinB=$\frac{5}{34}$$\sqrt{34}$得出sin∠ACD=$\frac{AC}{AD}$=$\frac{5}{34}$$\sqrt{34}$，即可求得AD：AC=$\sqrt{34}$：5；
（2）根据勾股定理求得AC和CD的关系，然后根据三角形面积求得AC的长，即可求得AD的长．

解答 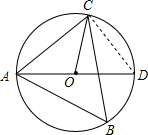解：（1）连接CD，
∵AD是直径，
∴∠ACD=90°，
∵∠ADC=∠B，
∴sinB=$\frac{5}{34}$$\sqrt{34}$=sin∠ACD=$\frac{AC}{AD}$，
∴AD：AC=$\sqrt{34}$：5；
（2）∵AD：AC=$\sqrt{34}$：5，
∴AD=$\frac{\sqrt{34}}{5}$AC，
∵AC²+CD²=AD²，
∴AC²+CD²=$\frac{34}{25}$AC²，
∴CD=$\frac{3}{5}$AC，
∴△AOC的面积为15，
∴△ACD的面积为30，
∴$\frac{1}{2}$AC•CD=30，
∴$\frac{1}{2}$AC•$\frac{3}{5}$AC=30，
∴AC=10，
∴AD=$\frac{\sqrt{34}}{5}$AC=2$\sqrt{34}$．

点评 本题考查了圆周角定理、勾股定理、解直角三角形等，找出辅助线构建直角三角形是解题的关键．