题目内容
10.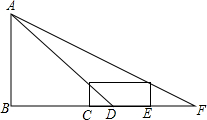 如图,小明同学晚上由路灯A下的B处走到C处时,测的影子CD的长为1.5米,继续往前走3米到达E处时,测的影子EF的长为2.5米,已知小明同学的身高是1.5米,求路灯AB的高度.
如图,小明同学晚上由路灯A下的B处走到C处时,测的影子CD的长为1.5米,继续往前走3米到达E处时,测的影子EF的长为2.5米,已知小明同学的身高是1.5米,求路灯AB的高度.
分析 根据GC=DC得∠GDC=45°可以证明△ABD是等腰直角三角形,设AB=x,根据$\frac{HE}{AB}=\frac{EF}{BF}$列出方程即可解决.
解答 解:∵GC=DC=1.5,GC⊥CD,AB⊥BD,
∴∠GDC=∠CGD=45°,∠BAC=90°-∠ADB=45°,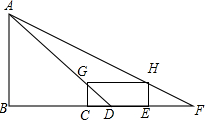
∴∠BAD=∠ADB,
∴BA=BD,设AB=x,则BC=x-1.5,
∵HE⊥BF,
∴HE∥AB,
∴$\frac{HE}{AB}=\frac{EF}{BF}$,
∴$\frac{1.5}{x}=\frac{2.5}{x-1.5+3+2.5}$,
x=6,
∴AB=6米.
点评 本题考查了相似三角形的应用:通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.

练习册系列答案
相关题目
15. 如图是一个正方体的展开图,在原正方体中和“国”字相对的面上的字是( )
如图是一个正方体的展开图,在原正方体中和“国”字相对的面上的字是( )
 如图是一个正方体的展开图,在原正方体中和“国”字相对的面上的字是( )
如图是一个正方体的展开图,在原正方体中和“国”字相对的面上的字是( )| A. | 中 | B. | 钓 | C. | 鱼 | D. | 岛 |
19.若把分式$\frac{x+3y}{2xy}$的x、y同时扩大10倍,则分式的值( )
| A. | 扩大为原来的10倍 | B. | 缩小为原来的$\frac{1}{10}$ | ||
| C. | 不变 | D. | 缩小为原来的$\frac{1}{5}$ |
 按图所示程序进行计算,第三次的运算结果是-101.
按图所示程序进行计算,第三次的运算结果是-101.
 如图,点A,B,C都在网格图中的格点上,则∠ABC的正切值$\frac{1}{2}$.
如图,点A,B,C都在网格图中的格点上,则∠ABC的正切值$\frac{1}{2}$.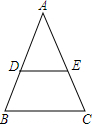 已知:如图,在△BAC中,AB=AC,D,E分别为AB,AC边上的点,且DE∥BC,求证:△ADE是等腰三角形.
已知:如图,在△BAC中,AB=AC,D,E分别为AB,AC边上的点,且DE∥BC,求证:△ADE是等腰三角形.