题目内容
2. 如图,点A,B,C都在网格图中的格点上,则∠ABC的正切值$\frac{1}{2}$.
如图,点A,B,C都在网格图中的格点上,则∠ABC的正切值$\frac{1}{2}$.
分析 首先连接AC,利用勾股定理计算出CA2,AB2,BC2,然后利用勾股定理逆定理可判定∠CAB=90°,再根据正切定义进行计算即可.
解答  解:连接AC,
解:连接AC,
∵CA2=12+12=2,AB2=22+22=8,BC2=12+32=10,
∴AC2+AB2=BC2,
∴∠CAB=90°,
∴tan∠ABC=$\frac{AC}{AB}$=$\frac{\sqrt{2}}{\sqrt{8}}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 此题主要考查了勾股定理逆定理,以及勾股定理,锐角三角函数定义,关键是正确判定△ABC是直角三角形.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
17. 如图,在△ABC中,D为BC上一点,E为AD延长线上一点,BD:DC=5:3,∠C=∠E,若AD=4,BC=8,则DE的长为( )
如图,在△ABC中,D为BC上一点,E为AD延长线上一点,BD:DC=5:3,∠C=∠E,若AD=4,BC=8,则DE的长为( )
 如图,在△ABC中,D为BC上一点,E为AD延长线上一点,BD:DC=5:3,∠C=∠E,若AD=4,BC=8,则DE的长为( )
如图,在△ABC中,D为BC上一点,E为AD延长线上一点,BD:DC=5:3,∠C=∠E,若AD=4,BC=8,则DE的长为( )| A. | $\frac{15}{4}$ | B. | $\frac{15}{3}$ | C. | 5 | D. | 3 |
14. 如图所示,A、B、C是同一直线上的依次三点,下列说法正确的是( )
如图所示,A、B、C是同一直线上的依次三点,下列说法正确的是( )
 如图所示,A、B、C是同一直线上的依次三点,下列说法正确的是( )
如图所示,A、B、C是同一直线上的依次三点,下列说法正确的是( )| A. | 射线AB与射线BA是同一条射线 | B. | 射线BA与射线BC是同一条射线 | ||
| C. | 射线AB与射线AC是同一条射线 | D. | 直线BA与直线BC不是同一条直线 |


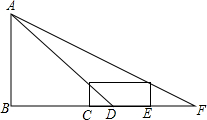 如图,小明同学晚上由路灯A下的B处走到C处时,测的影子CD的长为1.5米,继续往前走3米到达E处时,测的影子EF的长为2.5米,已知小明同学的身高是1.5米,求路灯AB的高度.
如图,小明同学晚上由路灯A下的B处走到C处时,测的影子CD的长为1.5米,继续往前走3米到达E处时,测的影子EF的长为2.5米,已知小明同学的身高是1.5米,求路灯AB的高度. 如图,正比例函数y=kx(k>0)的图象与反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y${\;}_{2015}=\frac{2015}{x}$的图象在第一象限内分别交于点A1,A2,…,A2015,点B1,B2,…,B2014分别在反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y${\;}_{2014}=\frac{2014}{x}$的图象上,且A2B1,A3B2,…,A2015B2014分别与y轴平行,连接OB1,OB2,…,OB2014,则△OA2B1,△OA3B2,…,△OA2015B2014的面积之和为1007.
如图,正比例函数y=kx(k>0)的图象与反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y${\;}_{2015}=\frac{2015}{x}$的图象在第一象限内分别交于点A1,A2,…,A2015,点B1,B2,…,B2014分别在反比例函数y1=$\frac{1}{x}$,y2=$\frac{2}{x}$,…,y${\;}_{2014}=\frac{2014}{x}$的图象上,且A2B1,A3B2,…,A2015B2014分别与y轴平行,连接OB1,OB2,…,OB2014,则△OA2B1,△OA3B2,…,△OA2015B2014的面积之和为1007. 如图,⊙O是△ABC的外接圆,点D在⊙O上,已知∠ACB=∠D,BC=3,则AB的长是3.
如图,⊙O是△ABC的外接圆,点D在⊙O上,已知∠ACB=∠D,BC=3,则AB的长是3.