题目内容
20．
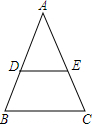已知：如图，在△BAC中，AB=AC，D，E分别为AB，AC边上的点，且DE∥BC，求证：△ADE是等腰三角形．
分析 根据等腰三角形的性质得到∠B=∠C，根据平行线的性质得到∠B=∠ADE，∠C=∠AED，等量代换得到∠ADE=∠AED，即可得到结论．
解答 证明：∵AB=AC，
∴∠B=∠C，
又∵DE∥BC，
∴∠B=∠ADE，∠C=∠AED，
∴∠ADE=∠AED，
∴AD=AE，
∴△ADE是等腰三角形．
点评 本题考查了等腰三角形的性质和判定，平行线的性质，三角形内角和定理，熟记定理与性质是解题的关键．
练习册系列答案
相关题目
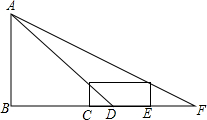如图，小明同学晚上由路灯A下的B处走到C处时，测的影子CD的长为1.5米，继续往前走3米到达E处时，测的影子EF的长为2.5米，已知小明同学的身高是1.5米，求路灯AB的高度．
8．用配方法解一元二次方程x2+4x-6=0，此方程可变形为（ ）
| A． | （x+2）2=10 | B． | （x-2）2=10 | C． | （x+2）2=2 | D． | （x-2）2=2 |
如图，在四边形纸片ABCD中，AD∥BC，AD＞CD，将纸片沿过点D的直线折叠，使点C落在AD上的点C′处，折痕DE交BC于点E，连结C′E．
如图，⊙O是△ABC的外接圆，点D在⊙O上，已知∠ACB=∠D，BC=3，则AB的长是3．
如图，已知A、O、E三点在同一条直线上，OB平分∠AOC，OD平分∠COE．