题目内容
已知:关于x的一元二次方程x2-3x-k=0有两个不相等的实数根x1、x2.
(1)求k的取值范围;
(2)若2(x1+x2)+x1x2+10=0,求k的值.
(1)求k的取值范围;
(2)若2(x1+x2)+x1x2+10=0,求k的值.
考点:根的判别式,根与系数的关系
专题:
分析:(1)根据根的判别式可得方程x2-x+m-2=0有两个不相等的实数根则△>0,然后列出不等式计算即可;
(2)先根据根与系数的关系得出x1+x2=3,x1x2=-k,再代入2(x1+x2)+x1x2+10=0,得出2×3-k+10=0进行计算即可.
(2)先根据根与系数的关系得出x1+x2=3,x1x2=-k,再代入2(x1+x2)+x1x2+10=0,得出2×3-k+10=0进行计算即可.
解答:解:(1)∵一元二次方程x2-3x-k=0有两个不相等的实数根,
∴△=b2-4ac=(-3)2-4×1×(-k)>0,
∴k>-
,
(2)∵关于x的一元二次方程x2-3x-k=0有两个不相等的实数根x1、x2,
∴x1+x2=3,x1x2=-k,
∵2(x1+x2)+x1x2+10=0,
∴2×3-k+10=0,
∴k=16.
∴△=b2-4ac=(-3)2-4×1×(-k)>0,
∴k>-
| 9 |
| 4 |
(2)∵关于x的一元二次方程x2-3x-k=0有两个不相等的实数根x1、x2,
∴x1+x2=3,x1x2=-k,
∵2(x1+x2)+x1x2+10=0,
∴2×3-k+10=0,
∴k=16.
点评:此题考查了根的判别式和根与系数的关系,一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根,根与系数的关系是x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
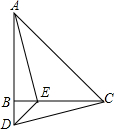 如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
 已知:如图,△ABC中,BC边中垂线ED交BC于E,交BA延长线于D,过C作CF⊥BD于F,交DE于G,DF=
已知:如图,△ABC中,BC边中垂线ED交BC于E,交BA延长线于D,过C作CF⊥BD于F,交DE于G,DF=