Question

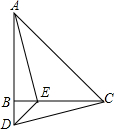如图，在△ABC中，AB=CB，∠ABC=90°，D为AB延长线上一点，点E在BC边上，且BE=BD，连结AE、DE、DC．
①求证：△ABE≌△CBD；
②若∠CAE=30°，求∠BDC的度数．

Answer 1

考点：全等三角形的判定与性质,三角形的外角性质

专题：证明题

分析：①利用SAS即可得证；
②由全等三角形对应角相等得到∠AEB=∠CDB，利用外角的性质求出∠AEB的度数，即可确定出∠BDC的度数．

解答：①证明：在△ABE和△CBD中，

AB=CB ∠ABC=∠CBD=90° BE=BD

，
∴△ABE≌△CBD（SAS）；
②解：∵△ABE≌△CBD，
∴∠AEB=∠BDC，
∵∠AEB为△AEC的外角，
∴∠AEB=∠ACB+∠CAE=30°+45°=75°，
则∠BDC=75°．

点评：此题考查了全等三角形的判定与性质，以及三角形的外角性质，熟练掌握全等三角形的判定与性质是解本题的关键．