题目内容
9.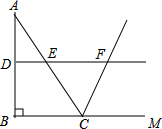 如图所示,在△ABC中,∠ABC=90°,AB=8,BC=6,若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,求线段DF的长.
如图所示,在△ABC中,∠ABC=90°,AB=8,BC=6,若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,求线段DF的长.
分析 根据勾股定理求出AB,根据三角形中位线定理求出DE、EC,根据角平分线的性质、平行线的性质解答.
解答 解:∵∠ABC=90°,AB=8,BC=6,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10,
∵DE是△ABC的中位线,
∴DE=$\frac{1}{2}$BC=3,DE∥BC,EC=$\frac{1}{2}$AC=5,
∵CF是∠ACM的平分线,
∴∠ECF=∠MCF,
∵DE∥BC,
∴∠EFC=∠MCF,
∴∠ECF=∠EFC,
∴EF=EC=5,
∴DF=DE+EF=3+5=8.
点评 本题考查的是三角形中位线定理和勾股定理的应用,掌握三角形的中位线平行于第三边,并且等于第三边的一半是解题的关键.

练习册系列答案
相关题目
17.为鼓励居民节约用电,某省试行阶段电价收费制,具体执行方案如表:
(1)若一户居民七月份用电420度,则需缴电费多少元?
(2)若一户居民某月用电x度(x大于200小于400),则需缴电费多少元?(用含x的代数式表示)
(3)某户居民五、六月份共用电500度,缴电费262元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小于400度,问该户居民五、六月份各用电多少度?
| 档次 | 每户每月用电数(度) | 执行电价(元/度) |
| 第一档 | 小于200部分 | 0.5 |
| 第二档 | 200小于等于400部分 | 0.6 |
| 第三档 | 大于400部分 | 0.8 |
(2)若一户居民某月用电x度(x大于200小于400),则需缴电费多少元?(用含x的代数式表示)
(3)某户居民五、六月份共用电500度,缴电费262元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小于400度,问该户居民五、六月份各用电多少度?
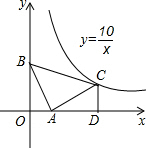 如图,在等腰直角三角形ABC中,∠BAC=90°,点A在x轴上,点B的坐标是(0,3).若点C恰好在反比例函数y=$\frac{10}{x}$第一象限内的图象上,过点C作CD⊥x轴于点D,那么点C的坐标为(5,2).
如图,在等腰直角三角形ABC中,∠BAC=90°,点A在x轴上,点B的坐标是(0,3).若点C恰好在反比例函数y=$\frac{10}{x}$第一象限内的图象上,过点C作CD⊥x轴于点D,那么点C的坐标为(5,2).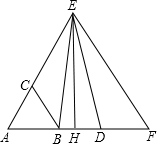 如图,已知D是等边三角形ABC的AB边延长线上一点,BD的垂直平分线HE交AC延长线于点E,那么CE与AD相等吗?试说明理由.
如图,已知D是等边三角形ABC的AB边延长线上一点,BD的垂直平分线HE交AC延长线于点E,那么CE与AD相等吗?试说明理由. 如图,若?ABCD的周长为36,过点D分别作AB,BC边上的高DE,DF,且DE=4,DF=5,求?ABCD的面积.
如图,若?ABCD的周长为36,过点D分别作AB,BC边上的高DE,DF,且DE=4,DF=5,求?ABCD的面积. 如图,在正方形ABCD中,E、F分别是AB,BC上一点,EG⊥AF于H,交CD于点G,求证:BE+BF=CG.
如图,在正方形ABCD中,E、F分别是AB,BC上一点,EG⊥AF于H,交CD于点G,求证:BE+BF=CG.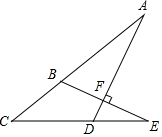 如图,已知EB⊥AD,垂足点为F,若∠C=40°,∠E=25°,则∠A=25°.
如图,已知EB⊥AD,垂足点为F,若∠C=40°,∠E=25°,则∠A=25°.