题目内容
20.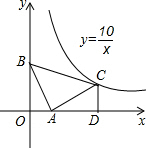 如图,在等腰直角三角形ABC中,∠BAC=90°,点A在x轴上,点B的坐标是(0,3).若点C恰好在反比例函数y=$\frac{10}{x}$第一象限内的图象上,过点C作CD⊥x轴于点D,那么点C的坐标为(5,2).
如图,在等腰直角三角形ABC中,∠BAC=90°,点A在x轴上,点B的坐标是(0,3).若点C恰好在反比例函数y=$\frac{10}{x}$第一象限内的图象上,过点C作CD⊥x轴于点D,那么点C的坐标为(5,2).
分析 由于∠BAC=90°,容易求证△ABO≌△CAD,利用全等三角形的性质即可求出点C的坐标.
解答 解:∵∠BAC=90°
∴∠BAO+∠CAD=∠CAD+∠ACD=90°,
∴∠BAO=∠ACD
在△ABO与△CAD中
$\left\{\begin{array}{l}{∠AOB=∠ADC}\\{∠BAO=∠ACD}\\{AB=AC}\end{array}\right.$
∴△ABO≌△CAD(AAS)
∴OB=AD
设OA=a,
∵B(0,3)
∴OB=3,
∴AD=3,
∴OD=a+3,CD=OA=a,
∴C(a+3,a)
又∵点C在反比例函数y=$\frac{10}{x}$上
∴10=a(a+3)
解得:a=2或a=-5,
∴C(5,2)
故答案为:(5,2)
点评 本题考查反比例函数图象上点的特征,解题的关键是证明△ABO≌△CAD,利用AD=OB=3求出点C的坐标,本题属于中等题型.

练习册系列答案
相关题目
9.下列各式计算正确的是( )
| A. | $2\sqrt{-8}=-2$ | B. | ${({-\sqrt{2}})^2}=4$ | C. | $\sqrt{{{({-3})}^2}}=-3$ | D. | $\sqrt{16}$=4 |
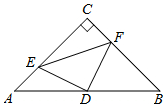 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:①△DFE是等腰直角三角形;②四边形CEDF不可能为正方形;③四边形CEDF的面积随点E位置的改变而发生变化;④点C、E、D、F四点在同一个圆上,且该圆的面积最小为4π.其中错误结论的个数是( )个.
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:①△DFE是等腰直角三角形;②四边形CEDF不可能为正方形;③四边形CEDF的面积随点E位置的改变而发生变化;④点C、E、D、F四点在同一个圆上,且该圆的面积最小为4π.其中错误结论的个数是( )个.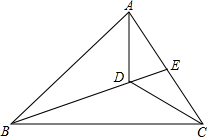 三角形不等式是指一个三角形的两边长度之和大于第三边的长度.在图中,E位于线段AC上,D位于线段BE上.
三角形不等式是指一个三角形的两边长度之和大于第三边的长度.在图中,E位于线段AC上,D位于线段BE上.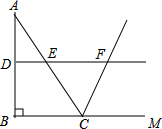 如图所示,在△ABC中,∠ABC=90°,AB=8,BC=6,若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,求线段DF的长.
如图所示,在△ABC中,∠ABC=90°,AB=8,BC=6,若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,求线段DF的长.