题目内容
14. 如图,在正方形ABCD中,E、F分别是AB,BC上一点,EG⊥AF于H,交CD于点G,求证:BE+BF=CG.
如图,在正方形ABCD中,E、F分别是AB,BC上一点,EG⊥AF于H,交CD于点G,求证:BE+BF=CG.
分析 过点E作EM⊥DC于点M,由正方形的性质和已知条件易证四边形EBCM是矩形,△ABE≌△EMG,进而可得到BE=CM,再由相等线段的代替即可证明BE+BF=CG.
解答 证明:
过点E作EM⊥DC于点M,则四边形EBCM是矩形,
∴BE=CM,BC=EM,
∵四边形ABCD是正方形,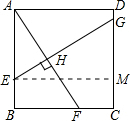
∴∠B=∠EMG=90°,AB=BC,
∵EG⊥AF于H,
∴∠GEM+∠EHA=90°,∠BAF+∠EHA=90°,
∴∠EAH=∠GEM.
在△ABE和△EMG中
$\left\{\begin{array}{l}{∠BAF=∠GEM}\\{AB=EM}\\{∠B=∠EMG=90°}\end{array}\right.$,
∴△ABE≌△EMG(ASA),
∴BF=GM,
∴CG=CM+GM=BE+BF.
点评 本题考查了正方形的性质、矩形的判断和性质、全等三角形的判断和性质,正确的作出辅助线构造全等三角形是证题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
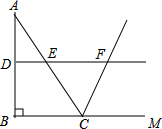 如图所示,在△ABC中,∠ABC=90°,AB=8,BC=6,若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,求线段DF的长.
如图所示,在△ABC中,∠ABC=90°,AB=8,BC=6,若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,求线段DF的长.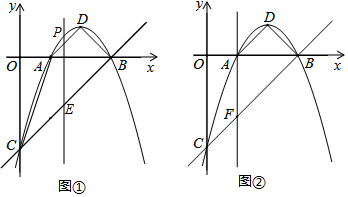
 某青少年科技创新小组设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两遥控车同时分别从A,B两处出发,沿轨道到达C处,设t(分)后甲、乙两遥控车与B处的距离分别为d1,d2,则d1,d2与t的函数关系如图所示,试根据图象解决下列问题:
某青少年科技创新小组设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两遥控车同时分别从A,B两处出发,沿轨道到达C处,设t(分)后甲、乙两遥控车与B处的距离分别为d1,d2,则d1,d2与t的函数关系如图所示,试根据图象解决下列问题: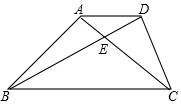 已知如图,在等腰Rt△ABC中,AB=AC,在等腰△BCD中,BC=BD,BD、AC相交于E,AD∥BC,求证:CD=CE.
已知如图,在等腰Rt△ABC中,AB=AC,在等腰△BCD中,BC=BD,BD、AC相交于E,AD∥BC,求证:CD=CE.