题目内容
某中学租用两辆小轿车(设速度相同)同时送一名带队老师及7名七年级的学生到某地参加数学竞赛,每辆车限坐4人(不包括司机).其中一辆小轿车在距离考场15km的地方出现故障,此时距离竞赛开始还有42分钟,唯一可利用的交通工具是另一辆小轿车,且这辆车的平均速度是60km/h,人步行的速度是12km/h(上、下车时间忽略不计)
(1)小明提议:可以让另一辆小轿车先送4名学生走,再返回来接我们.你认为小明的提议合理吗?通过计算说明理由.
(2)小强提议:可以让另一辆小车先送4名学生走,而其它4名师生同时步行前往,小轿车到达考场后再返回途中接送其他人.请你求出小轿车在距离考场多远与另4名师生相遇?
(3)按小强的建议这7名学生能在竞赛开始前进入考场吗?为什么?
(1)小明提议:可以让另一辆小轿车先送4名学生走,再返回来接我们.你认为小明的提议合理吗?通过计算说明理由.
(2)小强提议:可以让另一辆小车先送4名学生走,而其它4名师生同时步行前往,小轿车到达考场后再返回途中接送其他人.请你求出小轿车在距离考场多远与另4名师生相遇?
(3)按小强的建议这7名学生能在竞赛开始前进入考场吗?为什么?
考点:一元一次方程的应用
专题:
分析:(1)由于小汽车在距离考场15千米的地方出现故障,所以另一辆小汽车把自己车上的人送到市区后再回来送这一批人所走的路程应该为15×3,如果根据已知条件计算即可判断是否进考场的时刻前到达考场;
(2)设这车送4人到达后返回,再经过x小时后碰到另外步行的4人,那么车和步行的人是相遇问题,由此即可路程方程解决问题;
(3)求出到达考场所用的时间,再比较即可解答.
(2)设这车送4人到达后返回,再经过x小时后碰到另外步行的4人,那么车和步行的人是相遇问题,由此即可路程方程解决问题;
(3)求出到达考场所用的时间,再比较即可解答.
解答:解:(1)所需要的时间是:15×3÷60×60=45分钟,
∵45>42,
∴不能在截至进考场的时刻前到达考场.
(2)设车送4人到达后返回,再经过x小时后碰到另外步行的4人,则:
60x+12x=15-
×12,
有:x=
.
60×
=10千米,即在距离考场10千米处与另外4名师生相遇.
(3)所需要的时间是:
+2×
=
小时,
即35分钟,
∵35<42,
∴这7名学生能在竞赛开始前进入考场.
∵45>42,
∴不能在截至进考场的时刻前到达考场.
(2)设车送4人到达后返回,再经过x小时后碰到另外步行的4人,则:
60x+12x=15-
| 15 |
| 60 |
有:x=
| 1 |
| 6 |
60×
| 1 |
| 6 |
(3)所需要的时间是:
| 15 |
| 60 |
| 1 |
| 6 |
| 7 |
| 12 |
即35分钟,
∵35<42,
∴这7名学生能在竞赛开始前进入考场.
点评:本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.此题在设计方案的基础上,这样设计方案会更节省时间,汽车送第一批人的同时,第二批人先以12千米/时速度步行,汽车把第一批人送到距考场S千米的A处后,回来接第二批人.同时,第一批人也以12千米/时的速度继续赶往考场,使两批人同时到达考场,在汽车来回接人的过程中,多了第一批人在步行,显然所用时间比设计方案少,故此方案这8人都能赶到考场,且最省时间.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
借助一副三角尺,你能画出的角的度数是( )
| A、65° | B、15° |
| C、85° | D、95° |
 如图,△ABC中,E、D分别是AC、BC的中点,AD、BE交于点O,则S△DOE:S△AOB=( )
如图,△ABC中,E、D分别是AC、BC的中点,AD、BE交于点O,则S△DOE:S△AOB=( )| A、1:2 | B、2:3 |
| C、1:3 | D、1:4 |
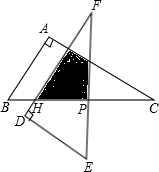 如图,△ABC中,∠A=90°,∠C=30°,BC=12cm,把△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置,DF交BC于点H.△ABC与△DEF重叠部分的面积为
如图,△ABC中,∠A=90°,∠C=30°,BC=12cm,把△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置,DF交BC于点H.△ABC与△DEF重叠部分的面积为 如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC
如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC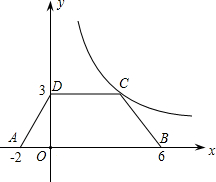 如图,等腰梯形ABCD放置在平面直角坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C.
如图,等腰梯形ABCD放置在平面直角坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C.